Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 38
a) Determine a potência média fornecida pela fonte de corrente senoidal no circuito da Figura P10.38.
b) Determine a potência média fornecida ao resistor de 20 V.
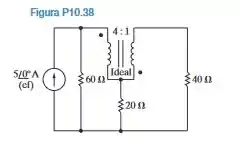
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Usando a transformação de Thevenin-Norton, o circuito resultante é igual a
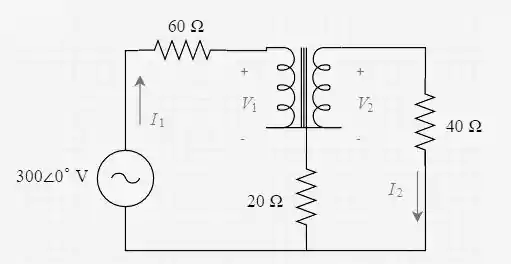
Aplicando a LKT no loop 1, nós temos que
Já no loop 2...
Da razão da transformação, nós obtemos o seguinte resultado
E
Substituindo (4) em (1) e (3), e (4) em (2) respectivamente, nós temos que
E
Passo 2
Resolvendo e de forma simultânea, nós temos que
E
E de e respectivamente
E
Passo 3
Aplicando a LKT no loop 1 para determinar a tensão aplicada pela fonte de corrente, isto é,
Fazendo as devidas substituições
Determinando a potência média fornecida pela fonte de corrente,
Substituindo os termos, nós temos que
Onde o sinal negativo indica que a potência média é fornecida pela fonte.
Passo 4
B – Aplicando LKC no nó A para poder determinar a corrente no resistor de , temos que
Substituindo os valores, nós temos que
Com isso, podemos determinar a potência média fornecida para o resistor
Logo, fazendo a substituição, nós obtemos o seguinte resultado