Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 22
Determine a tensão no capacitor como uma função do tempo para no circuito da figura. Considere condições de estado estacionário em .
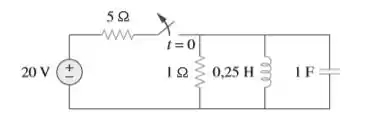
Passo 1
Acho interessante começar esse problema já considerando que a chave já está conectada ao por um tempinho já, então o circuito se resume ah...
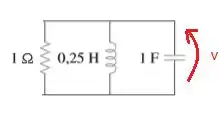
Onde Esse aí é quem devemos encontrar. Bora Resolver esse circuito então?
Passo 2
Bem, esse circuito pode ser resolvido usando a lei das correntes...
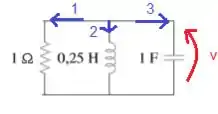
Onde a soma das correntes devem ser :
Ora, lembre-se de que a corrente no capacitor é ...
Derivando novamente...
Bora resolver essa EDO?
Passo 3
Beleza, então agora vamos resolvê-la aplicando a transformada de Laplace...
Ora, lembrando-se das Laplaces das derivadas...
Perceba então que temos que encontrar essas condições iniciais. Para isso, vamos utilizar aquelas informações lá sobre a chave no tempo !
Passo 4
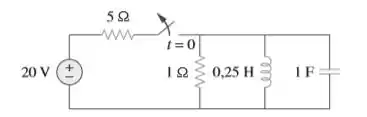
No ...
- Bobina é um curto o que implica em...
- A corrente na Bobina é então...
Após a abertura da chave , esses valores continuam já que a bobina não sofre variações bruscas de corrente e quanto ao capacitor, de tensão:
E
Da Equação do Capacitor, sabemos que...
Saca?
Passo 5
Voltando então para a equação...
Ganharemos essa daqui...
Isolando ...
E completando quadrados no denominador...
Esse cara se parece com a Laplace de seno, mas falta fazer uma jogada...
Prontinho! Podemos agora calcular a inversa encontrando o :