Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 25

Calcule v (t) para t > 0 no circuito da Figura.

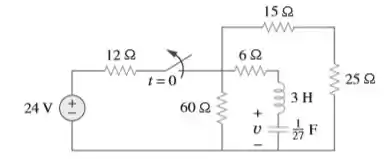
Passo 1

Acho interessante começar esse problema já considerando que a chave já está desconectada por um tempinho já, então o circuito se resume ah...

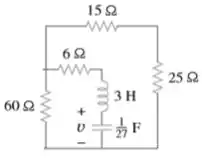
Onde esse v (t) aí é quem devemos encontrar. Bora resolver esse circuito então?

Passo 2

Bem, reparem primeiro que o ramo de 15 omega e 25 omega estão em paralelo com o de 60 :

60 // // ( 15 + 25 ) =

(60 (15 + 25))/(60 + 15 + 25) = 24

Então o circuito se reduz a...

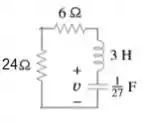
Esse circuito aí pode ser resolvido usando a lei das malhas se lembrando de que a tensão em cima do indutor é v_i = L d i // d t :

v (t) + 3 (d i (t))/(d t) + 3 0 i (t) = 0

Esse 30 é a soma dos dois resistores.

Ainda sabemos que a tensão em cima do capacitor é...

v (t) = (1)/(C) int_()^() i (t) d t ->

Derivando para tirar essa integral daí...

v^' (t) = (1)/(C) i (t)

Por fim, vamos só substituir o C = 1 // 27 ...

v^' (t) = 27 i (t)

Ou seja, as duas equações diferenciais que precisamos resolve são essas aqui:

v (t) + 3 (d i (t))/(d t) + 30 i (t) = 0

v^' (t) = 27 i (t)

Passo 3

Beleza, então agora vamos resolvê-las aplicando a transformada de Laplace (nas duas equações)...

L {v (t) + 3 (d i (t))/(d t) + 30 i (t)} = 0

L {v^' (t)} = 27 L {i (t)}

Ora, lembrando-se das Laplaces das derivadas...

V (s) + 3 (s I (s) - i (0)) + 30 I (s) = 0

s V (s) - v (0) = 27 I (s)

Perceba então que temos que encontrar essas condições iniciais. Para isso, vamos utilizar aquelas informações lá sobre a chave no tempo t = 0 !

Passo 4

Bem, no tempo t = 0 , a ainda está conectada...

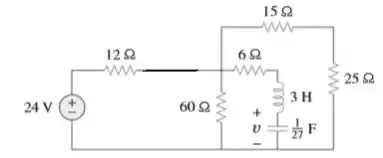
Mas como o indutor é um curto e o capacitor um circuito aberto em corrente continua, podemos reduzir o nosso circuito a:

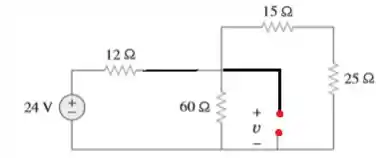
E a corrente só circula pelos outros ramos. Beleza! Então já sabemos que não circula corrente no indutor no momento da abertura, ou seja:

i (0) = 0

Mas e a condição v (0) ? Para isso, perceba que mesmo não havendo corrente, o capacitor tem uma tensão e que é igual à tensão no resistor de 60 . Vamos calcular essa tensão então!

Passo 5

Novamente perceba que os resistores de 25 e 15 estão em paralelo com o de 60 o que nos deu uma impedância equivalente de 24 :

60 // // ( 15 + 25 ) =

(60 (15 + 25))/(60 + 15 + 25) = 24

A corrente total demandada pela fonte é:

i_t = (24)/(12 + 24) = (2)/(3) A

Então a tensão que vai estar em cima do resistor de 60 omega é...

v = 24 - 12 * (2)/(3) =

16

E essa é a mesma tensão inicial do capacitor:

v (0) = 16

Passo 6

Podemos então voltar para as equações que precisamos resolver...

V (s) + 3 (s I (s) - i (0)) + 30 I (s) = 0

s V (s) - v (0) = 27 I (s)

Substituir os valores que encontramos...

V (s) + 3 (s I (s)) + 30 I (s) = 0

s V (s) - 16 = 27 I (s) o u I (s) = (1)/(27) s V (s) - (16)/(27)

Substituir I (s) na primeira equação...

V (s) + 3 ((1)/(27) s^2 V (s) - (16)/(27)) + 30 ((1)/(27) s V (s) - (16)/(27)) = 0 ->

V (s) + ((1)/(9) s^2 V (s) - (16)/(9)) + ((1 0)/(9) s V (s) - (16 0)/(9)) = 0 ->

Isolar...

V (s) (1 + (1)/(9) s^2 + (10)/(9) s) - (176)/(9) = 0 ->

V (s) (9 + s^2 + 10 s) - 176 = 0 ->

V (s) = (176)/((s^2 + 10 s + 9)) ->

Fatorar s^2 + 10 s + 9 em produto de dois termos...

V (s) = (176)/((s + 1) (s + 9)) ->

Por fim, separar em frações parciais onde vamos encontrar...

V (s) = (18)/(s + 1) + (- 2)/(s + 9) ->

v (t) , se agora aplicarmos a inversa!

v (t) = 18 e^(- t) - 2 e^(- 9 t)

Resposta

v (t) = 18 e^(- t) - 2 e^(- 9 t)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha v t para t0 no circuito da figura
No circuito da figura, a chave é movida (o contato é fechado antes de abrir o anterior) da posição A para B em t = 0 . Determine v t para qualquer t ≥ 0 .
A chave no circuito da figura que estava fechada a um longo tempo, é aberta em t = 0 . Determine i t para t0 .
A chave na figura é movida da posição A para B em t = 0 (observe que a chave deve ser conectada ao ponto B antes de interromper a conexão com A ) . Determine v t para t0 .
87- Desenvolva as equações de estado para o problema elaborado por você no Problema 16.13 .