Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 51
Determine a nos terminais do circuito da figura 6.73.
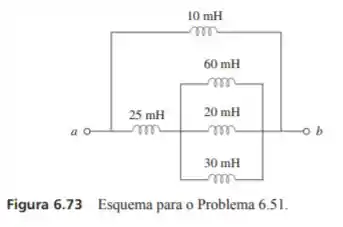
Passo 1
Para calcularmos a indutância equivalente devemos nos lembrar que para indutores vale a mesma ideia de resistores, ou seja, indutores em série nós somamos as indutâncias e indutores em paralelo nós somamos os inversos. Assim, vamos calcular primeiramente a associação de indutores em paralelo dada pelos indutores de e encontraremos
Agora, podemos calcular a indutância equivalente 2 dada por pois esses estão em série
Por fim, para concluirmos o exercício vamos calcular a equivalente final que é dada pela associação em paralelo dos indutores e e calculada da seguinte forma
Resposta
Exercícios de Livros Relacionados
Determine a capacitância equivalente da figura abaixo.
Para os dois capacitores em paralelo como indicados na figura abaixo, demonstre que a regra da divisão de corrente é: i 1 = C 1 C 1 + C 2 i s i 2 = C 2 C 1 + C 2 i s
Determine a capacitância equivalente da figura abaixo, consideranto que todos os capacitores sejam de 4μ F .
Demonstre que a regra de divisão de tensão para dois capacitores em série como na figura abaixo é: V 1 = C 2 C 1 + C 2 V s V 2 = C 1 C 1 + C 2 V s
Determine a capacitância equivalente da figura abaixo, consideranto que todos os capacitores sejam de μ F .