Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 61
Considere o circuito da figura 6.83. Determine:
se ;
;
a energia armazenada no indutor de em .
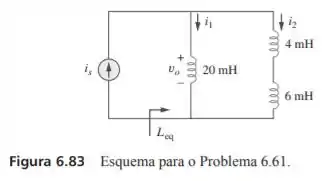
Passo 1
Para acharmos a indutância equivalente vamos proceder como se estivéssemos trabalhando com resistores. Assim, temos os resistores de em série e associado em paralelo com o indutor de e essa equivalente vai ser calculada como
Usando o divisor de corrente podemos encontrar facilmente que são dadas por
Passo 2
Agora, para achar vamos utilizar a equação do indutor e obteremos
Por fim, para finalizarmos o problema vamos calcular a energia necessária que é dada por
Resposta
Exercícios de Livros Relacionados
As indutâncias mostradas são todas em mH. Calcule a indutância equivalente vista pelos terminais a e b:
As indutâncias mostradas são todas em mH. Calcule a indutância equivalente vista pelos terminais a e b:
As indutâncias mostradas são todas em mH. Calcule a indutância equivalente vista pelos terminais:
Se o circuito está em regime permanente, em t = 0 - , calcule d v / d t e di/dt em t = 0 * .
Se v 0 - = 0 , calcule i ( 0 + ) e v ( 0 + ) .