Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 32

Elabore um problema para ajudar outros estudantes a entender melhor o fator de qualidade, a frequência de ressonância e a largura de banda de um circuito em paralelo.

Passo 1

Podemos determinar valores para , e em seguida encontrar o fator de qualidade , a frequência de ressonância , e a largura de banda

Vamos determinar , esses valores deve ser escolhidos aleartoriamente por nós nessa questão.

As fórmulas que iremos precisar são a de um circuito ressonante em paralelo, em resumo precisamos da fórmula da frequência de ressonância e a expressão geral do fator de qualidade. Elas são:

Passo 2

Encontramos a frequência de ressonância substituindo os valores que determinamos anteriormente na fórmula:

Passo 3

Encontrar o fator de qualidade , substituindo os valores na fórmula

Veja que podemos usar qualquer uma das igualdades que chegaremos ao mesmo resultado.

Passo 4

Por fim, vamos encontrar a largura de banda .

Como:

Então:

Passo 5

A melhor forma de entender os dados é esboçando um gráfico da amplitude vs frequência.

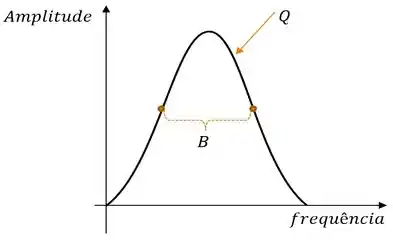
Quanto maior o fator de qualidade , menor será a largura de banda esse ajuste pode ser feito mudando os valores de .

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os parâmetros de circuito para um filtro rejeita-faixa R L C são: R=2k Ω , L=0,1H , C=40p F . Calcule:(a) A frequência central.(b) As frequências de meia potência.(c) O fator de qualidade.

Determine a transformada de Laplace de cada uma das seguintes funções:a) f ( t ) = t e - a t ;b) f ( t ) = s e n ω t ;c) f ( t ) = s e n ( ω t + u ) ;d) f ( t ) = t ;e) f ( t ) = c o s h ( t + u ) .

Use os teoremas do valor inicial e do valor final para verificar os valores inicial e final da corrente no Problema 12.28.

Não há nenhuma energia armazenada no circuito mostrado na Figura P12.27, no momento em que a chave é aberta. a) Deduza a equação íntegro-diferencial que governa o comportamento da tensão vo. b) Mostre

a) Use o teorema do valor inicial para determinar o valor inicial de v no Problema 12.26. b) O teorema do valor final pode ser usado para determinar o valor de regime permanente de v? Por quê?