Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 4
4. Elabore um problema para ajudar outros estudantes a entenderem melhor as potências instantânea e média usando a figura abaixo:
Passo 1
Bom! Esse é um problema pela qual nos teremos a responsabilidade de elaborar. Sendo assim, bora redesenhar esse circuito, atribuindo valores numéricos aos seus componentes:
O objetivo do problema é determinar a potência média dissipada nos resistores de e e comparar esse valor com o valor da potência complexa obtida para esse circuito.
E em seguida, bora fazer a análise nodal para esse circuito. Para isso, vamos redesenhá-lo mais uma vez, indicando as correntes, bem como nomeando os nós.
Aqui está...
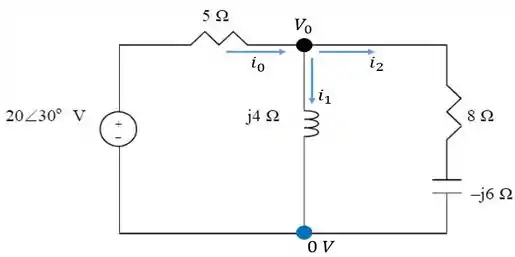
Aplicando a para esse nó superior, temos que:
E depois, substituindo as tensões nodais correspondentes a cada uma dessas correntes...
E com essa tensão , temos que a corrente que passa pelo resistor de , é igual a:
Onde a potência média, nesse caso, é dada por:
Passo 2
Continuando nosso raciocínio, bora calcular a corrente que circula no resistor de , e é dada por:
E a potência média dissipada nesse caso, no resistor de , vai valer...
Passo 3
Quanto a potência complexa, temos que ela é dada, utilizando a corrente como base; por...
E em seguida, bora determinar a potência média total dissipada nos dois resistores... Ela é igual à...
Como podemos ver, a potência média total dissipada pelos dois resistores, é praticamente igual à parte real da potência complexa obtida anteriormente. Conseguiu ver!?
Tudo ok por aqui!