Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Questões para revisão - Ex. 7
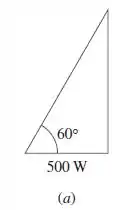
No triângulo de potência mostrado na Figura , a potência reativa é:
- adiantada
- atrasada
- adiantada
- atrasada
Passo 1
Galerano triângulo de potência apresentado, o lado oposto ao ângul ode representa a potência reativa, enquanto o lado adjacente é o de potência ativa. Assim,
Substituindo o valor de , temos:
Devido ao fato da potência aparente estar no primeiro quadrante, nós temos uma carga indutiva (a parte imaginária aqui é positiva!) e, portanto, uma potêcia reativa atrasada.
Resposta
A resposta é a letra (d).
Exercícios de Livros Relacionados
11. Para o circuito da figura 11.43 , suponha que a impedância da porta seja: Z = R 1 + ω 2 R 2 C 2 ∠ - tan - 1 ω R C Determine a potência média consumida pelo circuito quando R = 10k Ω , C = 200n F
17. Calcule o valor de Z L no circuito da figura 11.48 de modo que Z L receba a máxima potência média. Qual é a máxima potência média recebida por Z L ?
18. Determine o valor de Z L no circuito da figura 11.49 abaixo para a transferência de potência máxima.
19. O resistor variável R no circuito da figura 11.50 é ajustado até ele absorver a máxima potência média. Determine R e a máxima potência média absorvida.
21. Suponha que a impedância da carga seja puramente resistiva, que carga deveria ser conectada aos terminais a - b dos circuito da figura 11.52 , de modo que seja transferida a potência máxima para a