Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 13

13. A impedância de T h é v e n i n de uma fonte é Z T h = 120 + j 60   Ω , enquanto a tensão de T h é v e n i n de pico é V T h = 165 + j 0 V . Determine a potência máxima disponível da fonte.

Passo 1

Vamos montar o circuito equivalente de T h é v e n i n que o enunciado descreve:

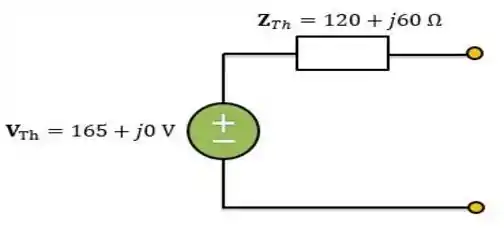
Passo 2

Agora é so lembrar que Z T h = R T h + j X T h e da fórmula:

P m a x = | V T h | 2 8 R T h

Sendo que...

| V T h | 2 = V T h ⋅ V T h *

| V T h | 2 = 165 ∠ 0 ° ⋅ ( 165 ∠ 0 ° )

| V T h | 2 = ( 165 ) 2

Ou seja, é so pegar o módulo do fasor e elevar ao quadrado.

Substituindo os valores correspondentes...

P m a x = ( 165 ) 2 8 ( 120 )

P m a x = 28,36   W

Resposta

P m a x = 28,36   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a leitura do wattímetro.
Dado i = i 1 + i 2 , onde i 1 = I 1 m cos ⁡ w 1 t i 2 = I 2 m cos ⁡ w 2 t É a corrente que flui no resistor R . Usando a definição do problema 12.13 , mostre, para w 1 ≠ w 2 , que P = P 1 + P 2 Onde P
Calcule o valor eficaz de uma corrente periódica para a qual um cicio e dado por:a) i = 3 tA 0 ≤ t ≤ 2 s 0 = 2t ≤ 4 s b) i = 6A0t2 s 0 = 2t8 s c) i = I m sin ⁡ 2 π t T A 0tT 2 0 = T 2tT s d) i = I m s
Mostre que, para 0 circuito do Ex. 15.4.1, a energia dissipada por ciclo e ∫ 0 2 π w 0 R I M 2 cos 2 ⁡ w 0 t d t = π R I M 2 w 0 e, desta forma, pela definição (15.27) e 0 resultado do Ex. 15.4.1. que
O amp op no circuito da Figura P10.7 é ideal. Calcule a potência média fornecida ao resistor de 1 kV, quando v g=c o s1.000 tV .