Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 53
Encontre a impedância vista pela fonte ideal de tensão no circuito da Figura P10.53, quando é ajustado para transferência de potência média máxima.
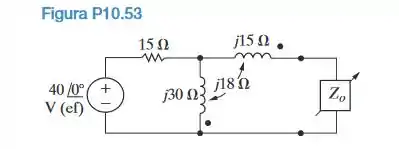
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Desconectando a impedância da carga , e com isso, determinando a tensão de Thevenin
Com isso, nós temos que
Que para fasores, está igual a
Agora, conectando os terminais da carga como um curto-circuito, nós temos duas malhas, com isso, nós temos que
E
De (2), nós obtemos a seguinte informação
Substituindo (3) em (1), para obter
Determinando a impedância equivalente de Thevenin
Com isso, nós temos que
Que passando para a forma retangular,
Passo 2
a impedância de carga na qual a potência média máxima é transferida para a carga é dada por
Conectando a impedância para o circuito equivalente de Thevenin, temos que a corrente fluindo através da carga é dada por
Substituindo os valores, nós temos que
Aplicando a LKT na malha 1 para determinar a corrente fornecida pela fonte de tensão
Portanto,
Substituindo
Transformando para fasores,
Onde é a corrente que flui através da impedância de carga, e é dada por,
Passo 3
Determinando a impedância vista pela fonte de tensão ideal
Substituindo