Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 51

51- Para o circuito interio da Figura 11.70 , calcule:

( a ) O fator de potência

( b ) A potência média liberada pela fonte

( c ) A potência reativa

( d ) A potência aparente

( e ) A potência complexa

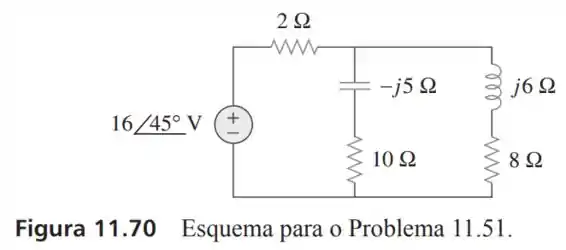
Passo 1

Para começar a respsonder essa questão nós precisamos descobrir a impedância equivalente desse circuito e ele pode ser vista como a soma da resistência de 2   Ω em série com o equivalente do paralelo entre 10 - j 5 e 8 + j 6 :

Z e q = 2 + 1 1 10 - j 5 + 1 8 + j 6 = 2 + ( 10 - j 5 ) ( 8 + j 6 ) 10 - j 5 + 8 + j 6

Z e q = 2 + 80 + 60 j - 40 j - 30 j 2 18 + j = 110 + 20 j 18 + j = 2 + 111.8 ∠ 10.3 18.03 ∠ 3.18 = 2 + 6.2 ∠ 7.12 °

Z e q = 2 + 6.2 cos ⁡ 7.12 + j 6.2 sin ⁡ 7.12 = 8.152 + j 0.768 = 8.188 ∠ 5.382 °

E como o ângulo do fator de potência depende exclusivamente do ângulo da reatância equivalente então:

F P = cos ⁡ 5.382 = 0.9956

Como a reatância tem caracterísitca é indutiva então o fator de potência é atrasado.

Passo 2

Agora para achar a potência média nós precisamos descobrir a potência total e ela será:

S = V R M S 2 Z * = 16 2 8.188 ∠ - 5.382 = 31.265 ∠ 5.382   V A

Com isso a potência total (ou aparente):

S = 31.265   V A

A fonte de 16   V está em RMS.

P = S cos ⁡ θ = 31.265 × 0.9956 = 31.13   W

Com isso a potência reativa será:

Q = S sin ⁡ θ = 31.265 × 1 - 0.9956 2 = 2.93   V A R

E a potência complexa será:

S = 31.13 + j 2.93 V A

Resposta

a )   F P = 0.9956

b )   P = 31.13   W

c )   Q = 2.93   V A R

d )   31.265   V A

e )   S = 31.13 + j 2.93 V A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

71- Três cargas são associadas em paralelo com uma fonte de 120 ∠ 0 °VR M S . A carga 1 absorve 60k V A R com F P = 0.85 atrasado, a carga 2 absorve 90k W e 50k V A R adiantada e a carga 3 absorve 100
72- Duas cargas conectadas em paralelo absorvem um total de 2.4k W com F P = 0.8 (atrasado) de uma linha de 120VR M S ,60H z . Uma carga absorve 1.5k W com F P = 0.707 (atrasado). Determine: a o F P d
83- As medições com um osciloscópio indicam que a tensão em uma carga e a corrente através dela são, respectivamente, 210 ∠ 60 °V e 8 ∠ 25 °A . Determine: ( a ) A potência real ( b ) A potência aparen
68- Calcule a potência complexa fornecida pela fonte de corrente no circuito R L C em série da Figura 11.87
67- Para o circuito com A O P da Figura 11.86 , calcule: a A potência complexa liberada pela fonte de tensão. ( b ) A potência média dissipada no resistor de 12Ω .