Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 13.Problemas - Ex. 40

Encontre as leituras dos wattímetros.

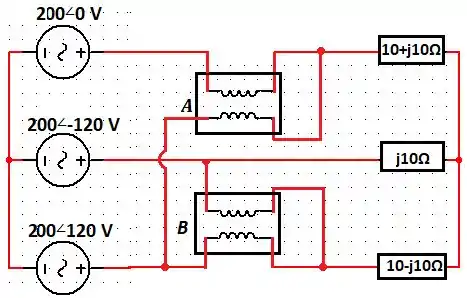
Passo 1

Ooooolha a última questão aeee, feraaa!!! Vamos que vamos!!

Vamos começar primeiro encontrando as correntes de linha em a e b , ou seja:

I_a = (V_a)/(Z_P) = (200 /_ 0 °)/(10 + j 10) = 10 sqrt(2) /_ - 4 5 ° A

I_b = (V_b)/(Z_P) = (200 /_ - 1 2 0 °)/(j 10) = 20 /_ 1 5 0 ° A

Além disso, o enunciado nos fala da tensão de linha e da sequência a b c . O que ele quer que saibamos é:

V_a b = (2 00 /_ - 3 0 °)/(sqrt(3)) V

V_b c = (200 /_ - 15 0 °)/(sqrt(3)) V

Passo 2

A leitura que o wattímetro A está lendo é dada por:

P_A = |V_a b| |I_a| cos (theta_V_a b - theta_I_a) :.

P_A = (200)/(sqrt(3)) xx 10 sqrt(2) cos (- 30 ° - ( - 4 5 ° )) :.

P_A = 422.65 W

Ainda, a leitura que o wattímetro B está lendo é dada por:

P_B = |V_c b| |I_c| cos (theta_V_c b - theta_I_c) :.

P_B = (200)/(sqrt(3)) xx 20 cos (- 1 5 0 ° - 1 5 0 °) :.

P_B = 1154.7 W

Resposta

P_A = 422.65 W

P_B = 1154.7 W

Exercícios de Livros Relacionados

7-a) Determine Io no circuito da Figura P11.7. b) Determine VAN. c) Determine VAB. d) O circuito é ou não um sistema trifásico equilibrado?Figura P11.7
12-O módulo da tensão de fase de uma fonte trifásica ideal, equilibrada, ligada em Y, é 125 V. A fonte está ligada a uma carga equilibrada, ligada em Y, por uma linha de distribuição que tem uma imped
Calcule a potência complexa em cada fase da carga não equilibrada do Problema 11.20.
A tensão fase-neutro no circuito da Figura P11.43 é 680 V, a sequência de fases é positivae a impedância de carga é 16 - j12 Ω / ϕ .a) Determine a leitura do wattímetro.b) Determine a potência reativa
As leituras dos wattímetros no circuito da Figura 11.20 são as seguintes: W1 = 40.823,09W e W2 = 103.176,91 W. O módulo da tensão de linha é 2.400 3 V. A sequência de fasesé positiva. Determine Z ϕ .