Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 4.8 - Ex. 3

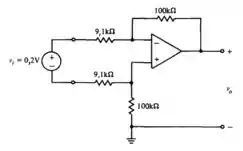
Escreva Vo, Vo/Vi , a resistência de entrada e a resistência de saída

Passo 1

Falaa galerinhaa!!! Tudo tranquilo?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para o determinar as tensões. Puts!! Já parece difícil?? Vai ser tranquilo. Partiu??

Pessoal, infelizmente ainda não tem essa matéria no Responde Aí, porém logo logo ela ainda vai ser produzida.

Então não vamos resolver essa questão?? Mas é claro que vamos, entretanto vamos resolver pelo método da análise nodal.

Com a análise nodal nosso circuito ficará o seguinte

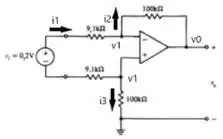
Agora já facilita muito a nossa visualização!!

Passo 2

Então bora láa!!

Vamos analisar esse circuito

Aplicando LKC vamos ter as seguintes relações

i 1 =   V i - V 1 9,1 k

i 2 =   V 1 - V 0 100 k

i 3 =   V 1 - 0 100 k

Aplicando LKC no nó V 1 , temos que

i 1 - i 2 = 0    

i 1 = i 2

Ou seja

V i - V 1 9,1 k   = V 1 - V 0 100 k  

9,1 k ( V 1 - V 0 ) =   100 k ( V i - V 1 )

V 0 =   100 k ( - V i + V 1 ) + 9,1 k V 1 9,1 k

Como já temos o valor de V i

V 0 =   100 k ( - 0,2 ) + 109,1 k V 1 9,1 k

V 0 =   - 20 k + 109,1 k V 1 9,1 k       . . . ( 1 )

Passo 3

Agora vamos para o último passo!!

Aplicando LKC no nó V 1 ( que está conectada ao terra) temos que

- i 1 - i 3 = 0      

i 1 = - i 3

Ou seja

V i - V 1 9,1 k   =   - V 1 100 k  

- 9,1 k V 1 =   - 100 k ( V i - V 1 )

- 90,9 k V 1 =   - 100 k V i

Substituindo os valore do enunciado

V 1 =   - 100 k ( 0,2 ) - 90,9 k

V 1   =   0,36   V

Agora, substituindo em (1)

V 0 =   - 20 k + 109,1 k ( 0,36 ) 9,1 k

V 0 =   - 2,198   V

Sendo assim

V 0 V i =   -   2,198   0,2 =   - 10,99   V

Resistência que está entrando no circuito

R e =   9,1 k   +   9,1 k   =   18,2   k Ω

Resistência que está saindo do circuito

R s =   0 Ω

Pronto!!

Resposta

V 0 =   - 2,198   V

V 0 V i =   - 10,99   V

R e =     18,2   k Ω

R s =   0   k Ω

Exercícios de Livros Relacionados

Calcule Vo em termos das tensões de nó V1, V2, e V3) e das resistências. (Este circuito é um somador, como o do Prob. 3.14, com uma fonte de tensão adicional.)
Calcule i.
Calcule v, se Vg = 8 cos 2t V. (Sugestão: Note que os terminais de entrada do amp. op. tem a mesma tensão de nó V1 como indicado.)
Calcule v se Vg = 8 sen 6t V.