Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 90
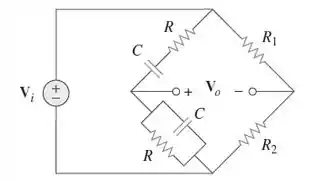
A Figura mostra um circuito com a ponte de Wien. Demonstre que a frequência na qual o deslocamento de fase entre os sinais de entrada e de saída é zero é dado por , e que o ganho necessário é nessa frequência.
Passo 1
Galera, a primeira coisa que vamos fazer é achar as impedâncias equivalentes. No ramo onde temos um resistor e um capacitor em série, temos:
No outro ramo, onde e são ligados em paralelo:
Passo 2
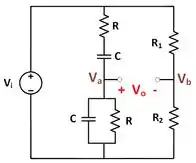
Vamos usar o divisor de tensão para encontrar a tensão (mostrado na figura abaixo).
Passo 3
Similarmente, pela divisão de tensão, nós podemos obter a tensão :
A tensão de saída é dada por:
Substituindo os valores:
Como ,
Passo 4
O deslocamento de fase entre os sinais de entrada e saída é zero quando o ganho é igual a um valor real, e isso ocorre quando:
Como ,
E o ganho nessa frequência se torna:
Pronto, conforme queríamos demonstrar! 😊
Resposta
Ei, a resposta está no passo a passo :)