Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 34
34. Use a análise de malhas para determinar a corrente na figura para o exemplo
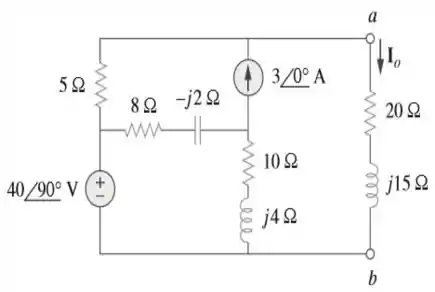
Passo 1
Fala galerinha! Não falei que ia voltar! Vamos pra mais um problema sobre circuitos com corrente alternada.
Olha só! Trata-se de um exemplo do nosso livro, que teremos de resolver aplicando a análise de malhas.
Bom! O livro foi bonzinho com a gente e já nos deu todos os seus elementos na forma fasorial.
Melhor pra gente, né não! Bora partir logo pra análise de malhas!
Passo 2
Nesse ritmo, o que temos que fazer é preparar o circuito pra utilizar a nossa análise de malhas. Quando digo preparar, é simplesmente nomear as correntes de malha!
Já vou me adiantando que tem supermalha aí no nosso desenho, hein! Tá vendo aquela corrente de ali, não!?
E aqui está nossa bela figura com todas as correntes de malha já indicadas, e a supermalha envolta por uma região pontilhada.
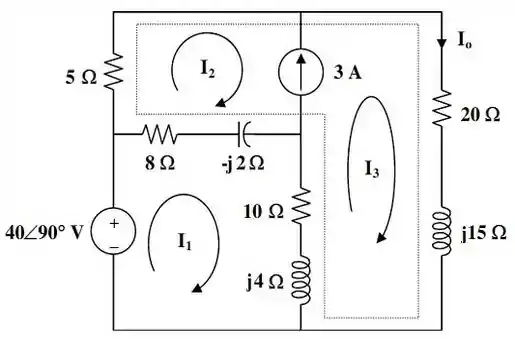
Desse modo... Aplicando a lei das tensões de para a malha , encontramos a seguinte equação:
Aplicando também a lei das tensões de para a supermalha, obtemos outra relação interessante:
Só que pela lei das correntes de nesse circuito, temos que:
Passo 3
Peguemos então, as equações e :
Somando as duas, alcançamos a seguinte relação:
Mas sabemos que:
Substituindo essa igualdade na equação anterior, chegamos a uma nova descoberta:
Dividindo por ...
A questão nos pede para achar apenas o valor de . E é ai que eu pergunto. Precisa a gente achar mais alguma outra corrente de malha?
É obvio que não! A corrente é a corrente de malha , que acabamos de encontrar. Basta ver que é que está circulando naquela parte mais livre do circuito, o ramo maior que contém um resistor e um indutor.
Logo...
Cumprimos nossa missão aqui! Até a próxima!