Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 36
36. Calcule no circuito da figura usando a análise de malhas.
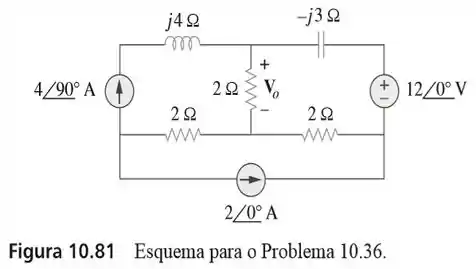
Passo 1
Fala galerinha! Vamos pra mais um problema sobre circuitos com corrente alternada.
Olha só! A questão foi boazinha com a gente e já nos deu todos os seus elementos na forma fasorial.
Bom pra gente, né não! Bora partir logo pra análise de malhas!
Passo 2
Nesse passo, vamos preparar o circuito pra utilizar a nossa análise de malhas. Quando digo preparar, é simplesmente nomear as correntes de malha!
E bora lá reformular esse circuito. Aqui está nossa bela figura:
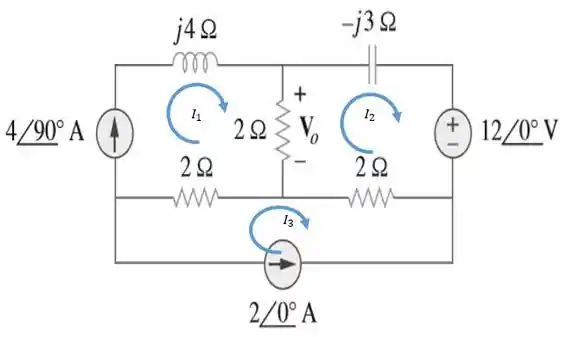
Olha só! Antes de ir pra análise de malhas, bora dar uma investigada nesse circuito. Reparou algo de interessante?
Ora bolas! A corrente de malha , é na verdade . Concluimos isso, vendo que a corrente de está circulando em um ramo livre dessa malha, sem a presença de nós.
E também tiramos que a corrente vai valer . O sinal negativo advém do fato de que a corrente está circulando em sentido oposto ao que adotamos para a corrente de malha nessa parte.
Depois disso, bora aplicar a lei das tensões de para a malha , de forma que encontramos a seguinte equação:
Como já conhecemos os valores de e , basta substituir na equação acima:
Passando para a forma retangular, de novo:
Passo 3
Tá quase acabando! Só falta obter !
Bom! Plea figura do enunciado e que redesenhamos no , podemos ver que:
Substituindo os valores correspondentes...
Alcançamos nossa resposta... Pra finalizar, bora colocar no domínio da frequência:
Cumprimos nossa missão aqui! Até a próxima!