Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 64
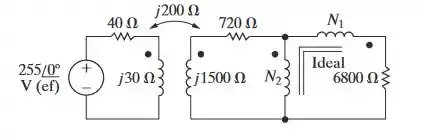
a) Se for igual a 1.000 espiras, quantas espiras deve ter o enrolamento do transformador ideal, no circuito apresentado na Figura P10.64, para que seja fornecida máxima potência média à carga de 6.800 V?
b) Determine a potência média fornecida ao resistor de 6.800 V.
c) Qual percentagem da potência média fornecida pela fonte de tensão ideal é dissipada no transformador linear?
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A - A partir da figura, vamos desativar a fonte de tensão e determinar a impedância equivalente de Thévenin vista nos terminais a, b.
Que é basicamente igual a
Em fasores...
Como a impedância vista nos terminais a, b em relação ao transformador de relação de espiras é real, a potência média máxima é transferida para o resistor de se e somente se,
Com isso, temos o seguinte circuito
Como o transformador de relação de espiras (N1/N2) é sem perdas, a impedância é dada por
De (1) e (2), nós podemos determinar o valor de
Desenvolvendo um pouco mais,
Portanto,
Logo,
Passo 2
B – Da figura 1, a tensão de Thevenin é dada por
Que no caso, será dada por
Que convertendo para fasores, é igual a
Como o transformador ideal é sem perdas, a potência média fornecida ao resistor é igual à potência média fornecida à impedância mostrada na Figura 2.
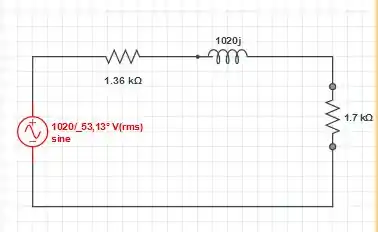
Determinando a corrente fluindo através da impedância
Substituindo os valores, nós temos que
Convertendo para fasores, nós temos que
Determinando a potência média transferida para a impedância
Novamente, fazendo a substituição dos resultados
Passo 3
C – Aplicando a LKT no loop 1 para conseguir a corrente fornecida pela fonte de tensão, nós temos que
Desenvolvendo um pouco mais os termos, nós temos que
Portanto,
A potência complexa fornecida pela fonte de tensão é dada por
Novamente, fazendo a substituição
A potência média fornecida pela fonte de corrente é dada por
A potência média dissipada na transformação linear é dada por
Com isso, nós temos que
Determine a porcentagem da potência desenvolvida pela fonte de tensão para aquela dissipada na transformação linear
Substituindo os valores, nós temos que