7 O resistor variável Ro no circuito da Figura P10.47 é ajustado até que absorva máxima potência média.
a) Qual é o valor de Ro em ohms?
b) Calcule a potência média fornecida a Ro.
c) Se Ro for substituído por uma impedância variável Zo, qual será a máxima potência média a ser fornecida a Zo?
d) Em (c), qual percentagem da potência produzida pelo circuito é fornecida à carga Zo?
Passo 1
Beleza pessoal?! Espero que sim pois iremos dar inicio a uma excelente resolução com o padrão de qualidade do Responde Aí. Pegue seu lápis e papel e vamos começar.
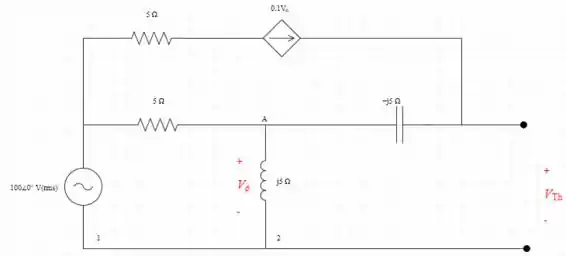
- Primeiro iremos desconectar o resistor , depois iremos aplicar a lei de Kirchoff no nó A e determinar a voltagem do
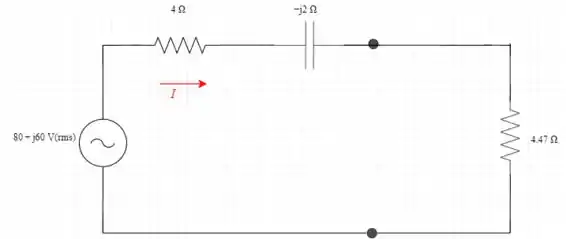
- Conecte o resistor de carga ao circuito equivalente de Thevenin como mostrado na figura
- A potência média máxima entregue à carga na condição de que a impedância de carga Zl seja dada por
- Conecte a impedância de carga , o circuito resultante é mostrado na Figura
Temos então,
Aplicando a lei de Kirchoff nó segundo loop para podermos determinar o valor da voltagem de Thevenin
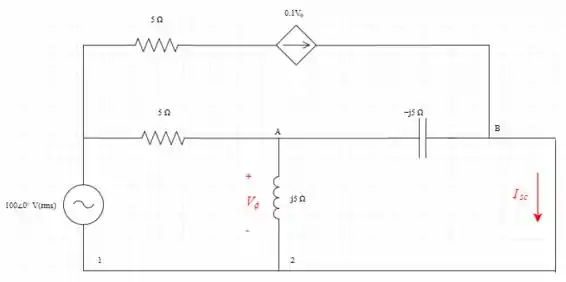
Conecte os terminais de carga via curto-circuito conforme mostrado na figura e aplicando a lei de Kirchoff no nó B
Aplicando a lei de Kirchoff no nó A
Então temos que
Substituindo (2) em (1) para determinar a corrente
Se você ainda não se perdeu, agora iremos calcular a impedância equivalente de Thévenin
Se apenas a magnitude da carga da impedância pode variar, mais do que a média da potência é transferida para a carga
Então, valor da resistência é dado por
Onde, é a impedância de carga na qual a potência média máxima é transferida para a carga, dada por
Passo 2
Determinar o fluxo da corrente através do resistor de
Determine a potência média máxima transferida para o resistor de carga
Passo 3
Agora iremos determinar a corrente que flui através da impedância de carga
determine a potência média máxima transferida para o resistor de carga
Determinar o valor da tensão
Aplicando a Lei de Kirchoff no nó B
Portanto, o valor da fonte de corrente dependente é dado por
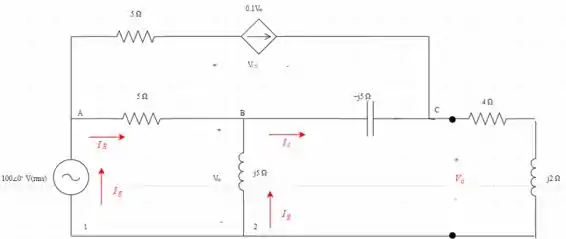
Aplicando a lei de Kirchoff no nó C para determinar a corrente do capacitor
A corrente flui através do indutor é dada por
Aplicando a lei de Kirchoff no nó B para descobrir a corrente que passa pelo resistor de
Aplicando agora no nó A para determinar a corrente entregue pela fonte
Agora iremos determinar a tensão do complexo de potência
Onde, o sinal negativo indica que a potência complexa é fornecida pela fonte de tensão
Aplicando a lei de Kirchoff no loop exterior iremos encontrar a voltagem da fonte dependente
Agora iremos determinar a corrente
Finalmente para quem me acompanhou até aqui, estamos chegando ao final.
A potência média desenvolvida no circuito Pdev é devida apenas à fonte de tensão,
Determine a porcentagem da potência média entregue à carga para aquela desenvolvida no circuito
Resposta
Veja o desenvolvimento meu caro amigo, muito importante para seu aprendizado.