Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 18
Se no circuito da Figura 12.49, determine, para a carga, as corrente de fase .
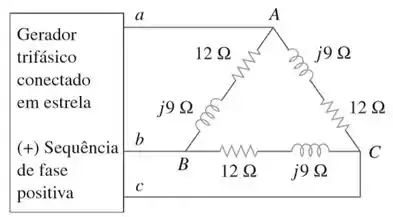
Passo 1
Com essa questão, temos um sistema estrela-delta. E a questão nos dá a tensão fase-neutro. Sabendo disso, vamos converter essa tensão fase-neutro em uma tensão de fase!
Passo 2
Legal? Agora vamos passar para as correntes de fase!
Resposta
Exercícios de Livros Relacionados
Para o circuito trifásico na Figura 12.59, determine a potência média absorvida pela carga conectada em triângulo com Z Δ = 21 – j24 Ω .
Uma fonte trifásica equilibrada com V L = 240 V RMS fornece 8 kVA com fator de potência 0,6 (atrasado) para duas cargas em paralelo ligadas em estrela. Se uma carga absorve 3 kW com fator de potência
Consulte a Figura 12.48. Obtenha a potência complexa absorvida pelas cargas associadas.
Um gerador trifásico equilibrado libera 7,2 kW para uma carga conectada em estrela de impedância 30 + j40 Ω por fase. Determine a corrente de linha I L e a tensão de linha V L .
Uma carga trifásica é formada por três resistores de 100 Ω que podem ser ligados em triângulo ou em estrela. Determine que conexão absorverá a maior potência média de uma fonte trifásica com tensão de