Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 43
Consulte a Figura 12.48. Obtenha a potência complexa absorvida pelas cargas associadas.
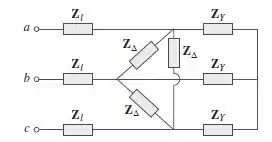
Passo 1
Para responder este problema devemos primeiro responder o exercício 12.15.
Visto que, a corrente de fase que passa pela carga é:
E a impedância da carga é:
Passo 2
Desse modo, a potência complexa pode ser obtida por:
Portanto,
Resposta
Exercícios de Livros Relacionados
No circuito trifásico equilibrado da Figura P11.43, a bobina de corrente do wattímetroestá ligada à linha aA e a bobina de potencial do wattímetro está ligada às linhas b e c. Mostreque a leitura do w
Um gerador trifásico ligado em D tem uma impedância interna de 9 + j90 m Ω / ϕ . Quandoo gerador opera a vazio, o módulo de sua tensão terminal é 13.800 V. O gerador alimentauma carga ligada em ∆ por
A Figura P11.21 mostra uma fonte trifásica, equilibrada, ligada em ∆ .a) Determine o circuito equivalente ligado em Y.b) Mostre que o circuito equivalente ligado em Y fornece a mesma tensão de circuit
Uma carga trifásica equilibrada absorve 150 kVA, com um fator de potência adiantado de0,96, quando a tensão de linha nos terminais da carga é 600 V. Determine quatro circuitosequivalentes que podem se
a) Determine a leitura de cada wattímetro no circuito da Figura P11.51, quando Z =13,44 + j46,08 Ω .b) Verifique se a soma das leituras dos dois wattímetros é igual à potência total fornecidaà carga.c