Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 4

Mostre que a função de transferência V_2 // V_1 é dada por:

H (s) = (V_2 (s))/(V_1 (s)) = ((1)/(R_1) s)/(s^2 + (1)/(R_2) s + (1)/(R_3))

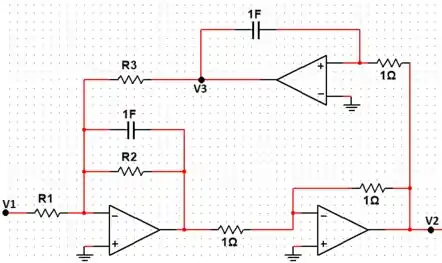
Passo 1

Diz aí que vc olhou para esse “circuitinho” e pensou:

Tenta sossegar e vamos devagarzinho que vai dar certo haha!!!

Sabemos que, para uma resistência R , a impedância é:

Z_R (s) = R

E, para uma capacitância C , sua impedância é:

Z_C (s) = (1)/(s C)

Assim, temos o seguinte circuito (considerando as características das entradas do amp op e supondo direções de corrente):

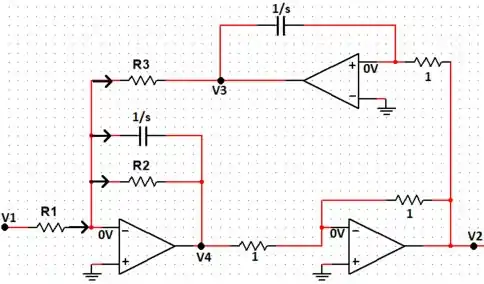
Passo 2

Analisando o circuito acima, percebemos que:

(V_3)/((1)/(s)) = - (V_2)/(1) :. V_3 = - (V_2)/(s)

E que:

(V_4)/(1) = - (V_2)/(1) :. V_4 = - V_2

Passo 3

Assim, fazendo a Lei dos Nós, já substituindo V_3 e V_4 :

(V_1)/(R_1) = (V_2)/(R_2) + (V_2)/((1)/(s)) + ((V_2)/(s))/(R_3) :.

(V_1)/(R_1) = V_2 ((1)/(R_2) + s + (1)/(s R_3)) :.

(V_1)/(V_2) = R_1 ((s R_3 + s^2 R_2 R_3 + R_2)/(s R_2 R_3)) :.

(V_2)/(V_1) = ((s)/(R_1))/(s^2 + (s)/(R_2) + (1)/(R_3)) = H ( s )

Resposta

H (s) = ((s)/(R_1))/(s^2 + (s)/(R_2) + (1)/(R_3))

Exercícios de Livros Relacionados

Mostre que H s é a função de rede de um filtro corta-faixa e calcule H j ω M A X , ω 0 , ω c 1 e ω c 2 .
Calcule a frequência de ressonância para o circuito RLC paralelo descrito por (a) R = 2 Ω k , L = 4 m H e C = 0,1 μ F ; (b) ω d = 5r a d / s e α = 12N p / s ; e (c) α = 1N p / s , R = 4 Ω e L = 2 H .
a) Usando os valores dos componentes do apêndice H, combine, pelo menos, um resistor, um indutor e um capacitor em série para criar uma impedância de 300 - j400 Ω a uma frequência de 10.000 rad/s. b)
Determine a admitância Y a b no circuito visto na Figura P9.23. Expresse Y a b em forma polar e também em forma retangular. Determine o valor de Y a b em milissiemens.
a) Mostre que, a uma dada frequência ω , os circuitos na Figura P9.20(a) e (b) terão a mesma impedância entre os terminais a,b se R 1 = R 2 1 + ω 2 R 2 2 C 2 2 C 1 = 1 + ω 2 R 2 2 C 2 2 ω 2 R 2 2 C 2