Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 58
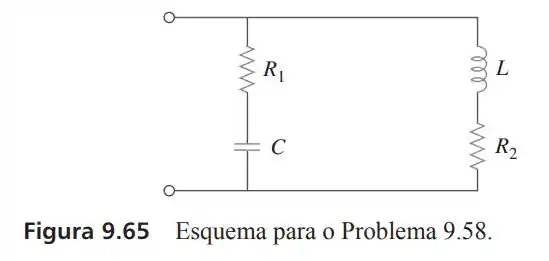
58- Usando a Figura , elabore um problema para ajudar outros estudantes a entender melhor as associações e impedâncias:
Passo 1
Vamos dizer que a frequência angular desse circuito vale , para valores de capacitor igual a:
Além de:
Descubra a impedância total desse circuito.
As reatâncias do capacitor e do indutor será:
Passo 2
Note que temos duas impedâncias em paralelo uma valendo e a outra sendo , então a impedância total será calculada por:
Fazendo essa conta
Onde :
Transformando tanto o numerador quanto o denominador em fasores nós teremos:
Agora repassando para a forma complexa:
Resposta
Exercícios de Livros Relacionados
Calcule os parâmetros z e os parâmetros ABCD do circuito mostrado na figura abaixo.
Calcule a função de transferência de ganho de tensão para o quadripolo terminado em 1 Ω , mostrado na Fig. 14.16, com parâmetros z: Z 11 = 6 Ω , Z 12 = Z 21 = 4 Ω e Z 22 = 10 Ω .
Use os parâmetros ABCD para calcular V 2 / V 1 para o quadripolo terminado em um resistor de 1Ω se o quadripolo e a rede T da Fig. 14.13 com Z 1 = Z 2 = 2 s e Z 3 = 1 / s .
Calcule V 2 / V g , para o circuito mostrado abaixo.
Para o circuito R L C em serie com uma fonte de tensão v g , faça a função de rede ser H=I / V g , ondeI e a corrente fasorial. Mostre que as respostas em amplitude e fase são similares as da Fig. 15.