Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 11.Problemas - Ex. 39

A potência total fornecida a uma carga trifásica equilibrada, quando submetida a uma tensão

de linha de 2.500 3 V, é 900 kW, com um fator de potência atrasado de 0,6. A impedância da

linha de distribuição que alimenta a carga é de 1 + j3 Ω / ϕ   . Sob tais condições de funcionamento, a queda do módulo da tensão de linha entre o início e o final da linha é excessiva. Para compensar, um banco de capacitores, ligados em Y, é inserido em paralelo com a carga. O banco de capacitores é projetado para fornecer 1.125 kVAR de potência reativa,

quando alimentado por uma tensão de linha de 2.500 3 V.

a) Qual será a magnitude da tensão no início da linha quando a tensão de linha nos terminais da carga for 2.500 3 V e o banco de capacitores estiver desligado?

b) Repita (a), com o banco de capacitores ligado.

c) Qual é a eficiência percentual da linha em relação à potência média em (a)?

d) Qual é a eficiência em (b)?

e) Se o sistema estiver operando com uma frequência de 60 Hz, qual será o valor de

cada capacitor em microfarads?

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe circuitos trifásicos equilibrados!

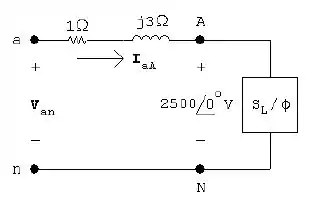
  1. Podemos ilustrar o sistema da seguinte forma:

    2. Para esse item, temos que:

    S L / ϕ = 1 3 900 + j 900 0,6 ( 0,8 ) 10 3 = 300000 + j 400000   k V A

    Também:

    I a A * = 300000 + j 400000 2500 → I a A = 120 - j 160 A

    Para as tensões:

    V a n = 2500 + 1 + j 3 120 - j 160 = 3106,44 / 3,69 ° V

    Logo, o módulo:

    V a b = 3106,44 3 = 5380,5   V

    Passo 2

  2. Usando o resultado do item a, temos que I 1 = 120 - j 160 A ;

    3. Precisamos ainda de:

    S 2 = 0 - j 1 3 1125 x 10 3 = - j 375000   V A R

    Isso nos dá que:

    I 2 * = - j 375000 2500 → I 2 = j 1 50 A

    Com isso:

    I a A = 120 - j 10 A

    A tensão será:

    V a n = 2500 + 120 - j 10 ( 1 + j 3 ) = 2673,01 / 7,52 ° V

    Logo, o módulo:

    V a b = 2673,01 3 = 4629,8   V

  3. Para esse item, temos que:

    4. I a A = 200 A → P p e r d a / ϕ = 200 2 1 = 40   K W

    Logo:

    P g / ϕ = 300000 + 40000 = 340   k W

    Por fim:

    % n = 300 340 100 = 88,2 %

    Passo 3

  4. Para esse item, temos que:

    5. I a A = 120,416 A → P l / ϕ = 120,416 2 1 = 14500   K W

    Por fim:

    % n = 300 000 3 14500 100 = 95,4 %

  5. O valor de cada capacitor será:

Z c a p Y = 2500 2 j 375000 = - j 16,67   Ω

Sabendo que:

1 C ω = 16,67 → C = 159,155 μ F

Resposta

  1. Item a:

    2. V a b = 3106,44 3 = 5380,5   V

  2. Item b:

    3. V a b = 2673,01 3 = 4629,8   V

  3. Item c:

    4. % n = 300 340 100 = 88,2 %

  4. Item d:

    5. % n = 300000 314500 100 = 95,4 %

  5. Item e:

C = 159,155 μ F

Exercícios de Livros Relacionados

12-O módulo da tensão de fase de uma fonte trifásica ideal, equilibrada, ligada em Y, é 125 V. A fonte está ligada a uma carga equilibrada, ligada em Y, por uma linha de distribuição que tem uma imped
Calcule a potência complexa em cada fase da carga não equilibrada do Problema 11.20.
A tensão fase-neutro no circuito da Figura P11.43 é 680 V, a sequência de fases é positivae a impedância de carga é 16 - j12 Ω / ϕ .a) Determine a leitura do wattímetro.b) Determine a potência reativa
As leituras dos wattímetros no circuito da Figura 11.20 são as seguintes: W1 = 40.823,09W e W2 = 103.176,91 W. O módulo da tensão de linha é 2.400 3 V. A sequência de fasesé positiva. Determine Z ϕ .
Deduza as equações 11.56 e 11.57.