Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 6
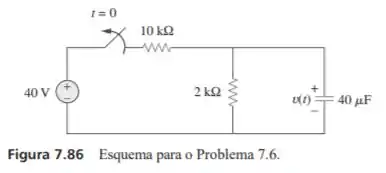
A chave da figura 7.86 foi fechada há um bom tempo e é aberta em . Determine para .
Passo 1
Primeiramente devemos encontrar a condição inicial para a tensão, ou seja, aplicando o divisor de tensão então temos
Encontraremos agora a constante de tempos que para um circuito é dada por
Por fim, conseguimos equacionar fazendo
Resposta
Exercícios de Livros Relacionados
A chave do circuito na Figura P7.57 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. No instante em que a chave faz contato com o terminal b, a chave 2 ab
O circuito da Figura P7.56 está em operação por um longo tempo. Em t = 0, a fonte de tensão inverte a polaridade e a fonte de corrente cai de 3 mA para 2 mA. Determine vo (t) para t $ 0.
a) Use os valores dos componentes do Apêndice H para criar um circuito RC de primeira ordem (veja a Figura 7.21) com uma constante de tempo de 250 ms. Use um único capacitor e uma rede de resistores,
A chave do circuito mostrado na Figura P7.22 esteve aberta por um longo tempo antes de seu fechamento em t = 0. Escreva a expressão para a tensão do capacitor, v(t), para t $ 0.
Depois de o circuito da Figura P7.33 estar em funcionamento por um longo tempo, uma chave de fenda é inadvertidamente colocada entre os terminais a, b. Suponha que a resistência da chave de fenda seja