Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 9.Problemas - Ex. 25

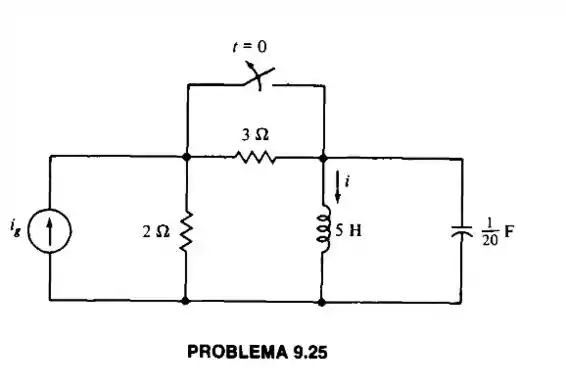
Calcule para , se e o circuito está em regime permanente em .

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Para análise de , como o circuito está em regime permanente, nós temos que

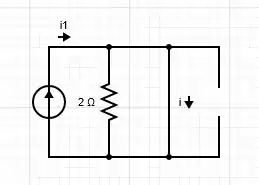
Logo, já sabemos que no instante 0,

Passo 2

Vamos converter a fonte de corrente para uma fonte de tensão, a fim de deixar todo mundo em série, e com isso, ser um RLC série, logo, temos a seguinte configuração de circuito

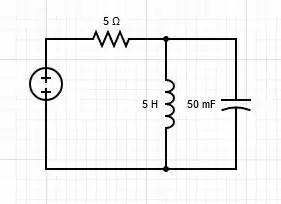
Ok, vamos calcular a partir disto, com isso, nós temos que

Logo

Tirando o delta, como se fosse uma EDO mesmo, nós temos que

Logo, o será igual a

Passo 3

Logo, a equação da corrente pode ser da seguinte forma, por suposição (é realmente um palpite muito certeiro na maioria dos casos)

Pegando a corrente no instante t = 0, temos que

E a tensão no indutor é dada por

Com isso, nós temos que

Portanto

Logo, temos que

Resposta

Resposta nos passos

Exercícios de Livros Relacionados

Se as raízes da equação característica de um circuito RLC forem –2 e –3, a resposta é:(a) ( Ac o s2 t+Bs e n2 t ) e - 3 t (b) A+ 2 B t e - 3 t (c) A e - 2 t + B t e - 3 t (d) A e - 2 t + B e - 3 t ond

Um circuito RLC em série possui R = 20 k Ω , L = 0,2 mH e C = 5 μ F. Que tipo de amortecimento é apresentado pelo circuito?

Elabore um problema para ajudar outros estudantes a entenderem melhor como funcionam os circuitos RLC sem fonte.

A resposta natural de um circuito RLC é descrita pela equação diferencial d 2 v d t 2 + 2 d v d t + v = 0 Para a quual as condições iniciais são v 0 = 10V , d v 0 d t = 0 . Calcule v ( t ) .

A corrente em um circuito RLC é descrita por d 2 i d t 2 + 10 d i d t + 25 i = 0 Se i(0) = 10 A, di(0)/dt =0 determine i(t) para t0.