Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 46

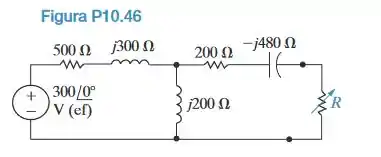
O resistor variável no circuito da Figura P10.46 é ajustado até que a potência média que ele absorve seja máxima.

a) Determine R.

b) Determine a máxima potência média.

c) Encontre um resistor no Apêndice H que teria a maior potência média fornecida a ele.

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

A – Desativando a fonte de tensão e determinando a impedância de Thevenin Z t h

Z t h = 200 - j 80 + j 200     500 + j 300

Desenvolvendo os termos,

Z t h = 200 - j 80 + j 200 500 + j 300 500 + j 500 = 240 - j 320   Ω

Passando para fasores,

Z t h = 400 ∠ - 53,13 °   Ω

Se apenas a magnitude da carga puder ser variada, a maior parte da potência média será transferida para a carga. Então, o valor da resistência R é dado por

R = Z L = Z t h

Logo,

R = 400   Ω

Passo 2

B – Desconectando a resistência R e determinando a tensão de Thevenin V t h através dos terminais da carga

V t h = j 200 500 + j 300 + j 200 300 ∠ 0 °

Com isso, nós temos que

V t h = 60 + j 60   V ( r m s )

Determinando a corrente I fluindo através do resistor da carga

I = V t h Z t h + R

Substituindo os valores, nós obtemos o seguinte resultado

I = 60 + j 60 640 - j 320 = 37,5 - j 112,5   m A ( r m s )

Passando para fasores,

I = 118,59 ∠ 71,57 °   m A ( r m s )

Determinando a potência média máxima transferida para o resistor de carga P

P = I 2 R

Com isso, nós temos que

P = 0,11589 2 400 = 5,625   W

Portanto,

P = 5,625   W

Passo 3

C – Do apêndice H, o resistor de valor mais próximo é de 390   Ω , com isso, vamos determinar a corrente fluindo através do resistor

I = V t h Z t h + R H

Substituindo os valores na equação, nós temos que

I = 60 + j 60 630 - j 320

Com isso, temos que I em fasores, é igual a

I = 120,084 ∠ 71,93 °   m A ( r m s )

A potência média máxima transferida para o resistor de carga P é

P = I 2 R

Fazendo a substituição

P = 0,120084 2 390 = 5,624   W

Portanto,

P = 5,624   W

Resposta

a )   R = 400   Ω

b )   P = 5,625   W

c )   P = 5,624   W

Exercícios de Livros Relacionados

40- Elabore um problema para ajudar outros estudantes a entender melhor a potência aparente e o fator de potência.
38- Para o sistema de potência da Figura 11.67 , determine: ( a ) potência média; ( b ) potência reativa; ( c ) fator de potência. Note que 220V é uma valor R M S
47- Para cada um dos casos a seguir, determine a potência complexa, a potência média e a potência reativa: c V = 80 ∠ 60°VR M S ,Z = 50 ∠ 30°Ω
47- Para cada um dos casos a seguir, determine a potência complexa, a potência média e a potência reativa: ( b ) v t = 160 cos ⁡ 377 tV ; i t = 4 cos ⁡ 377 + 45 ° A
46- Para os fasores de tensão e corrente a seguir, calcule a potência complexa, a potência aparente, a potência real e a potência reativa. Especifique se o F P está adiantado ou atrasado. d )V = 160∠