Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 45
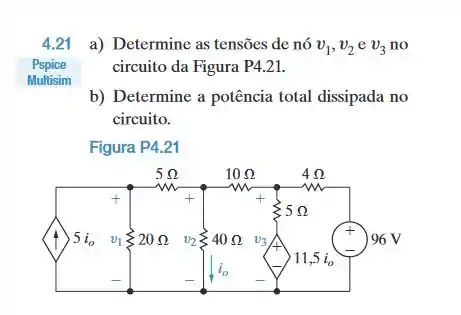
Resolva o Problema 4.21 usando o método das correntes de malha
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A - Deixando a corrente fluindo na malha esquerda ser , a segunda malha esquerda como , da terceira como e na malha direita como . Aplicando o método das correntes na segunda malha esquerda
Desenvolvendo os termos um pouco mais, nós temos que
Na terceira malha à esquerda, nós temos que
Com isso,
E na malha direita,
E com isso
Tendo uma expressão para , nós obtemos o seguinte resultado
Substituindo nas equações
Passo 2
Resolvendo o sistema de equações, nós temos que
Conseguindo o valor de , nós temos que
Substituindo os valores, nós temos que
Calculando o valor de
Substituindo os valores, nós temos que
Para o caso de
Substituindo os valores,
E finalmente, calculando o valor de
Substituindo os valores, nós temos que
Passo 3
B - Calculando a potência total dissipada no circuito pelos resistores e pela fonte de tensão dependente
Substituindo os valores, nós temos que
Logo, a potência dissipada é igual a