Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas Abrangentes - Ex. 86

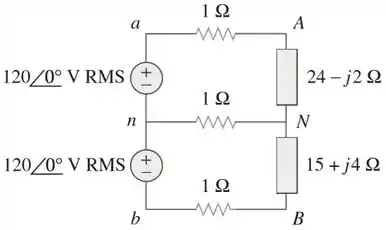
Para o sistema monofásico trifilar na Figura 12.77, determine as correntes I a A ,   I b B   e   I n N .

Passo 1

Vamos pra cima, galerinha! Primeiramente, vamos considerar o circuito abaixo!

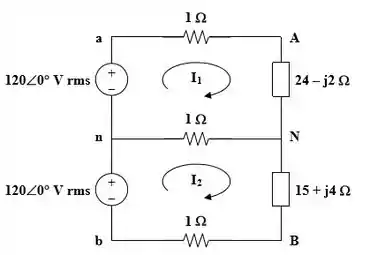
Para as duas malhas (1 e 2 respecitivamente), temos que:

120 = 26 - j 2 I 1 - I 2

120 = 17 + j 4 I 2 - I 1

Passo 2

Fazendo essas formulas para a forma de matrizes, temos que:

120 120 = 26 - j 2 - 1 - 1 17 + j 4 I 1 I 2

Sabendo disso, temos que:

Δ = 449 + j 70 ,     Δ 1 = 120 18 + j 4 ,     Δ 2 = ( 120 ) ( 27 - j 2 )

Simplificando isso em forma das correntes, temos que:

I 1 = Δ 1 Δ = 120 × 18.44 ∠ 12.53 ° 454.42 ∠ 8.86 ° = 4.87 ∠ 3.67 °

I 1 = Δ 1 Δ = 120 × 18.44 ∠ 12.53 ° 454.42 ∠ 8.86 ° = 4.87 ∠ 3.67 °

Portanto, temos que:

I a A = I 1 = 4.87 ∠ 3.67 ° A

I b B = - I 2 = 7.15 ∠ 166.9 ° A

Passo 3

Logo, para acharmos a corrente no neutro basta fazemos a diferença entre as correntes!

I n N = I 2 - I 1 = Δ 2 - Δ 1 Δ = I n N = 120 × 9 - j 6 449 + j 70 = 2.856 ∠ - 42.55 °

Resposta

I n N = 2.856 ∠ - 42.55 °

I a A = 4.87 ∠ 3.67 ° A

I b B = 7.15 ∠ 166.9 ° A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma fonte trifásica conectada em estrela equilibrada com V p = 210VR M S alimenta uma carga trifásica conectada em estrela com impedância por faseZ A=80Ω ,Z B=60+j 90ΩeZ C=j 80Ω . Calcule as correntes
Determine as correntes de linha para o circuito trifásico da Figura 12.64. Seja Va = 110 0 , Vb = 110l 120 e Vc = 110 120 V.
Considere a Figura 12.63 e elabore um problema para ajudar outros estudantes a entender melhor os sistemas trifásicos não equilibrados.
Determine as correntes de linha para o circuito trifásico da Figura 12.64. Seja V a = 110 ∠0 °,V b = 110 ∠ -120°eV c = 110 ∠120 °V .
Resolva o Problema 12.10 usando o PSpice ou MultiSim.