Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 54

Uma fonte trifásica conectada em estrela equilibrada com V p = 210   V   R M S alimenta uma carga trifásica conectada em estrela com impedância por fase   Z A   =   80   Ω ,   Z B   =   60   +   j 90   Ω   e   Z C   =   j 80   Ω . Calcule as correntes de linha e a potência complexa total liberada para a carga. Suponha que os neutros estejam interligados.

Passo 1

Vamos lá galera! A questão nos dá que a fonte é equilibrada, então quanto a isso é de boas! Quanto a carga, temos que:

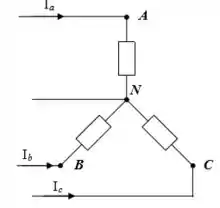
É bem simples de calcular nesse caso galera! Basta a gente dividir a tensão por cada carga!

Passo 2

Pois bem, vamos pras continhas!

I a = 210 ∠ 0 ° 80 = 2 , 625   A

I b = 210 ∠ - 12 0 ° 60 + j 90 = 210 ∠ - 120 ° 108 , 17 ∠ 56 , 31 ° = 1 , 9414 ∠ - 176,31 °

I c = 210 ∠ 12 0 ° j 80 = 2 , 625 ∠ 3 0 °   A

Sabendo disso,

S a = V I a * = 210 × 2 , 625 = 551 , 25

S b = V I b * = 210 ∠ - 120 °   . 1 , 9414 ∠ - 176 , 31 °   *

S b = 210 ∠ - 120 °   . 1,9414 ∠ + 176,31 °

S b = 407,694 ∠ 56,31 ° = 226,148 + j 339,222    

S c = V I c * = 210 ∠ 120 °   .   2,625 ∠ 30 ° *

S c = 210 ∠ 120 °   . 2,625 ∠ - 30 °

S c = 551,25 ∠ 9 0 ° = j 551,25  

Portanto, a potencia aparente é:

S = S a + S b + S c

S = 551,25 + 226,148 + j 339,222 + ( j 551,25 )

S = 777,4 + j 890,47   V A

Resposta

I a = 2 , 625   A

I b = 1,9414 ∠ - 176,31 ° A

I c = 2,625 ∠ 30 °   A

S = 777 , 4 + j 890 , 47   V A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a Figura 12.61 e elabore um problema que ajude outros estudantes a entender melhor sistemas trifásicos não equilibrados.
Um circuito estrela-estrela quadrifilar possui V a n = 120 ∠ 120 ° , V b n = 120 ∠ 0 ° V c n = 120 ∠ - 120 °V se as impedâncias forem Z A N = 20 ∠ 60 ° , Z B N = 30 ∠ 0 ° Z C N = 40 ∠ 30 °Ω Determine
Considere o sistema triângulo-triângulo mostrado na Figura 12.60. Adote Z 1 = 8 + j6 Ω , Z 2 = 4,2 – j2,2 Ω e Z 3 = 10 + j0 Ω .(a) Determine as correntes de fase I A B , I B C e I C A .(b) Calcule as
Considere a Figura 12.68 e elabore um problema para ajudar outros estudantes a entender melhor como usar o PSpice ou MultiSim para analisar circuitos trifásicos.