Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 22
Supondo que , desenhe um circuito RLC que tenha a equação característica seguinte
Passo 1
Relaxa, galera. Vamo se Ligar e achar a Resposta. Questão bem tranquila pessoal! Comparando com as caracteristiacas da eq (8.8), temos que:
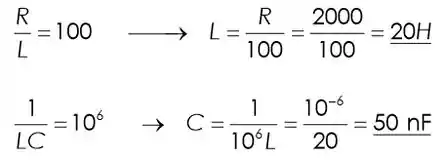
Disso, obtemos:
Resposta
Exercícios de Livros Relacionados
Elabore um problema para ajudar outros estudantes a entenderem melhor como funcionam os circuitos RLC sem fonte.
A resposta natural de um circuito RLC é descrita pela equação diferencial d 2 v d t 2 + 2 d v d t + v = 0 Para a quual as condições iniciais são v 0 = 10V , d v 0 d t = 0 . Calcule v ( t ) .
A corrente em um circuito RLC é descrita por d 2 i d t 2 + 10 d i d t + 25 i = 0 Se i(0) = 10 A, di(0)/dt =0 determine i(t) para t0.
Se R=50Ω , L=1,5H , qual valor de C tornará um circuito R L C em série:(a) com amortecimento supercrítico(b) com amortecimento crítico (c) com subamortecimento
A equação que descreve a tensão em um circuito RLC é d 2 v d t 2 + 5 d v d t + 4 v = 0 Se v(0) = 0, dv(0)/dt = 10 V/s, obtenha v(t).