Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 10.4 - Ex. 3

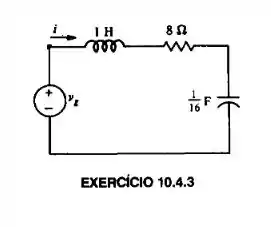
Usando o método de excitação complexa, calcule a resposta forçada i , se v g = 20 cos ⁡ 2 t   V .

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Ok, o método de excitação ele se baseia em exponenciais, até aí tudo tranquilo, até porque nós conseguimos senoides em termos que dependem de exponenciais. Para o caso em questão, nós temos as seguintes informações

v g = 20 cos ⁡ 2 t   V

Com essa informação, nós vamos fazer um palpite, em que a corrente i seja dada pela seguinte fórmula

i = A e j 2 t  

Vamos supor isso, agora vamos aplicar a LKT para o circuito, que nos fornece algo bem interessante

L d i d t + R i + 1 C ∫ 0 t i   d τ = 20 e j 2 t

Aqui nesse caso, nós já fizemos a conversão exponenciais complexas, vamos manipular um pouco mais, aplicando uma derivada em toda a equação, temos que

L d 2 i d t 2 + R d i d t + 1 C i = 40 j e j 2 t

É essa a equação diferencial que a gente vai brincar um pouquinho.

Passo 2

O indutor tem valor de 1 Henry, logo, podemos tirar de jogada para deixar essa segunda derivada sem nenhum termo proporcional (ou seja, eu só quero a derivada)

d 2 i d t 2 + R d i d t + 1 C i = 40 j e j 2 t

Lembra que a gente fez um palpite de solução? Pois bem, é hora de testar, substituindo na derivada, com isso, nós temos que

d 2 A e j 2 t d t 2 + R d A e j 2 t d t + 1 C A e j 2 t = 40 j e j 2 t

Substituindo os valores dos componentes passivos, nós obtemos a seguinte configuração de EDO

d 2 A e j 2 t d t 2 + 8 d A e j 2 t d t + 16 A e j 2 t = 40 j e j 2 t

Portanto, fazendo as derivadas

4 j 2 A e j 2 t + 2 j A e j 2 t + 16 A e j 2 t = 40 j e j 2 t

Vamos brincar um pouco mais no próximo passo...

Passo 3

Colocando o termo A e j 2 t em evidência, nós temos que

A e j 2 t - 4 + 16 j + 16 = 40 j e j 2 t

Podemos tirar e j 2 t da equação, para simplificar as coisas, com isso

A - 4 + 16 j + 16 = 40 j

Logo, A será igual a

A = 40 j 12 + 16 j = 40 ∠ 90 ° 20 ∠ 53,13 °

Logo

A = 2 ∠ 36,9 °  

Portanto, a corrente no domínio do tempo é igual a

i t = 2 cos ⁡ ( 2 t + 36,9 ° )   A

Resposta

i t = 2 cos ⁡ ( 2 t + 36,9 ° )   A

Exercícios de Livros Relacionados

Para o circuito RLC serie com excitação v g = v m cos ⁡ w tV , mostre que w 0 = 1 L C e Q = w 0 L R . A resposta é corrente de laço.
Use o método desta seção para esboçar as respostas em amplitude e em fase H s = 16 s s 2 + 4 s + 2504
Altere em escala a frequência e a impedância do circuito da Fig. 15.4 para obter w c = 2000 π r a d s( f c = 1000H z ) usando capacitores de 0,01e0,005μ F .
Mostre que, para a figura do Problema 15.4 H s = V 3 ( s ) V 1 ( s ) = - 1 R 1 s 2 + 1 R 2 s + 1 R 3 Escolha valores para as resistências de forma que o circuito seja um filtro passa-baixas butterwort
Se o ganho de um filtro passa-baixas com função de rede H ( s ) e definido como K = | H ( 0 ) | , compare os ganhos nos casos gerais dos Problemas 15.13 e 15.19, que são, respectivamente, circuitos pa