Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.10 - Ex. 2

Use os parâmetros ABCD para calcular V 2 / V 1 para o quadripolo terminado em um resistor de 1Ω se o quadripolo e a rede T da Fig. 14.13 com Z 1 = Z 2 = 2 s e Z 3 = 1 / s .

Passo 1

Iae, meus queridos! Td certinho??

Para essa questão é importantíssimo ter em mente a tabela de conversões de parâmetros de quadripolos.

Pela descrição do problema, temos o seguinte circuito:

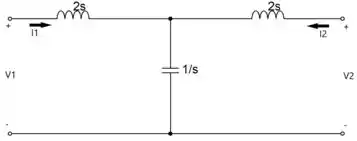
Para calcular V 2 / V 1 , vamos utilizar a equação 14.69.

V 2 V 1 = 1 A + B

Primeiramente vamos calcular os parâmetros z desse quadripolo, pra isso, vamos escrever as equações de malhas:

V 1 s = 2 s I 1 s + 1 / s I 1 s + I 2 s   V 2 s = 2 s I 2 s + 1 / s I 1 s + I 2 s

V 1 s = ( 2 s + 1 / s ) I 1 s + 1 / s I 2 s   V 2 s = 1 / s I 1 s + ( 2 s + 1 / s ) I 2 s

Com isso, vemos que...

Z 11 = Z 22 = 2 s + 1 / s Z 12 = Z 21 = 1 / s ou 2 s + 1 / s 1 / s 1 / s 2 s + 1 / s

Calculando o determinante da matriz acima, podemos encontrar o Δ Z , vamos usá-lo futuramente.

Δ Z = Z 11 Z 22 - Z 12 Z 21

Δ Z = ( 2 s + 1 / s ) ( 2 s + 1 / s ) - ( 1 / s ) ( 1 / s )

Δ Z = 4 s 2 + 4

Passo 2

Nesta etapa vamos converter os valores dos parâmetros em z para ABCD, pra isso vamos lembrar da tabela de conversão de parâmetros, onde podemos ver que...

A = Z 11 Z 21 B = Δ Z Z 21 C = 1 Z 21 D = Z 22 Z 21

Segundo a equação 14.69, precisamos apenas dos parâmetros A e B para calcular V 2 / V 1 , logo...

A = Z 11 Z 21 → A = 2 s + 1 s 1 s

A = 2 s 2 + 1

B = Δ Z Z 21 → B = 4 s 2 + 4 1 s

B = 4 s 3 + 4 s

Por fim, substituindo A e B na equação 14.69 temos...

V 2 V 1 = 1 2 s 2 + 1 + 4 s 3 + 4 s

V 2 V 1 = 1 4 s 3 + 2 s 2 + 4 s + 1

Foi tranquilo, né? Bora pra mais uma!

Resposta

V 2 V 1 = 1 4 s 3 + 2 s 2 + 4 s + 1

Exercícios de Livros Relacionados

10.27. Calcule o valor da corrente i em regime permanente.
10.35. Calcule a corrente i em regime permanente.
10.37. Calcule a corrente i em regime permanente, se Vg = 2 cos 4000t V.
10.36. Calcule a tensão v em regime permanente, se Vg = 10 cos 1000t V.
10.29. Calcule as correntes em regime permanente i e i1 usando fasores.