Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 98
Os valores dos parâmetros no circuito da Figura P7.97 são ; ; ; C = 250 pF e R = 23.083 .
a) Faça um gráfico de em função de t, admitindo que, depois de momentaneamente fechada, S permanece aberta até que o circuito atinja seu estado permanente. Admita que S seja fechada em t = 0. Faça o gráfico para o intervalo .
b) Repita (a) para em função de t.
Passo 1
Faaala, galerinha!! Como vocês estão? Partiu resolver mais uma questãozinha?
Para resolvermos o item (a), podemos observar que para , .
Sendo assim, quando a chave é momentaneamente fechada, salta para
Desse modo, permanecerá aberto por:
Portanto, o gráfico se dá por:
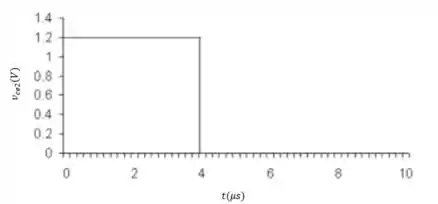
Passo 2
Já no item (b), para repetirmos o item (a) para em função de , devemos primeiramente encontrara o valor no intervalo de :
Além disso:
Por fim, plotando o gráfico de em função de t, temos que:
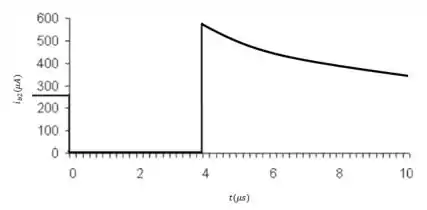
Prontinho, pessoal!! Bora resolver mais uma questão juntos?
Resposta
a)
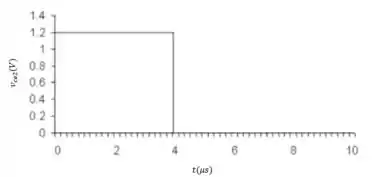
b)
