Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 9.Problemas - Ex. 25
a) Usando os valores dos componentes do apêndice H, combine, pelo menos, um resistor, um indutor e um capacitor em série para criar uma impedância de 300 - j400 a uma frequência de 10.000 rad/s.
b) Em que frequência o circuito da parte (a) tem uma impedância que é puramente resistiva?
Passo 1
Faaaaala, pessoal!! Bora resolver mais uma questão juntos?
Para esse exercício, vamos começar desenvolvendo o item (a):
Além disso, temos que:
Então:
Escolhemos L=10 mH. Então:
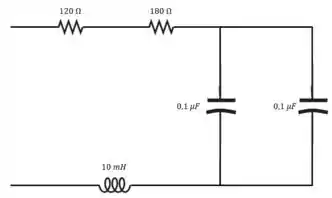
Podemos alcançar a capacitância desejada combinando dois capacitores de em paralelo. O circuito final é mostrado aqui:
Passo 2
Em seguida, para determinarmos a frequência que o circuito da parte (a) tem uma impedância que é puramente resistiva, faremos o seguinte:
Prontinho, pessoal!! Bem tranquilo, não é mesmo? Bora resolver mais uma questão juntos?
Resposta
a)
b) .