A placa de um transformador monofásico de e indica que ele tem uma tensão nominal de . Um ensaio de circuito aberto é executado a partir do lado de baixa tensão, e as respectivas leituras nos instrumentos de medida são e . Do mesmo modo, um ensaio de curto-circuito, no lado de baixa tensão, fornece leituras de e .
Calcule a impedância equivalente em série, a resistência e a reatância do transformador referidas aos terminais de baixa tensão.
Calcule a impedância equivalente em série do transformador referida aos terminais de alta tensão.
Fazendo as aproximações apropriadas, desenhe um circuito equivalente para o transformador.
Determine o rendimento e a regulação de tensão se o transformador estiver operando na tensão e carga nominais (fator de potência unitário).
Repita a parte , supondo que a carga tenha um fator de potência de capacitivo.
Passo 1
De acordo com o enunciado, as medidas obtidas nos ensaios do transformador de e foram:
Circuito aberto (No lado de BT):
Curto circuito (No lado de BT):
Passo 2
Com os valores do ensaio em curto circuito, podemos calcular a impedância equivalente série:
Logo, a impedância equivalente série será:
Passo 3
A relação de transformação desse transformador pode ser calculada utilizando as tensões nominais do transformador:
Então, a impedância equivalente referida ao lado de alta (secundário) será:
Passo 4
Na letra , temos que desenhar um circuito equivalente para o transformador, como o abaixo:
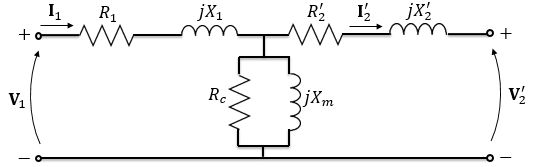
Vamos desenhá-lo referente ao primário, já que todas as medidas feitas nos ensaios foram feitas pelo lado de baixa.
Fazendo a aproximação necessária, temos:
Passo 5
Para completarmos o modelo, ainda falta encontrarmos os valores dos parâmetros do ramo de excitação. Para isso, temos que usar as medidas obtidas no ensaio de circuito aberto e aplicar nas fórmulas:
Passo 6
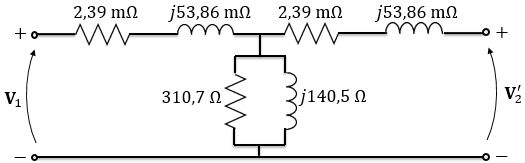
Agora que temos os valores de todas as resistências e reatâncias, podemos desenhar o modelo abaixo:
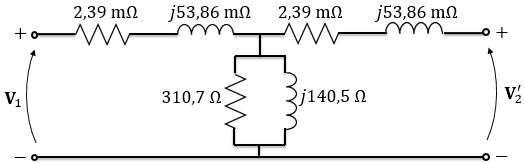
Passo 7
A regulação de tensão é calculada pela seguinte fórmula:
Para o cálculo de regulação de tensão podemos desconsiderar os parâmetros transversais (ramo de excitação) e considerar o modelo série do transformador:
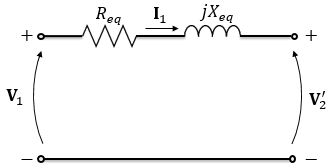
Já tínhamos calculado que:
Então, conectando a carga com fator de potência unitário, temos o circuito abaixo:
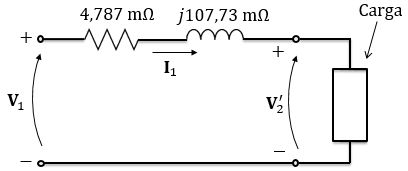
Na letra , o enunciado disse que o transformador está operando com seus valores nominais de tensão e corrente, ou seja, que a carga está sendo alimentada pelos valores nominais.
Então, vamos considerar que a tensão da carga está na referência, ou seja, seu ângulo é zero e como o valor nominal de tensão do primário é , temos:
Como o transformador alimenta uma carga com e com a corrente nominal, temos:
Logo,
Passo 8
Agora é aplicar a lei das tensões de Kirchhoff na malha do circuito:
Então, em nosso circuito, quando a carga está ligada, a tensão nos terminais do secundário é igual à tensão que está sendo aplicada na carga. Logo,
Agora, vamos analisar a condição sem carga. Quando não há carga conectada ao secundário, ou seja, quando o transformador está a vazio, temos o circuito abaixo:
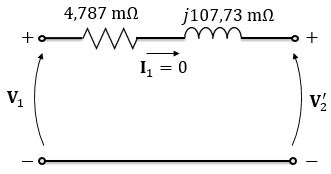
Como o circuito está aberto, não tem circulação de corrente, logo não há queda de tensão nas impedâncias do circuito e toda a tensão aplicada pela fonte conectada no primário é aplicada nos terminais do secundário. Logo,
Então, a regulação de tensão desse sistema será:
Passo 9
O rendimento de um transformador é calculado pela seguinte fórmula:
Em que a potência de entrada é a soma da potência de saída somado com as perdas.
A potência de saída é a potência ativa na carga. Como o fator de potência é unitário a potência ativa é igual a potência aparente.
Então, como a potência aparente nominal do transformador é .
Já as perdas estão relacionadas às perdas que ocorrem no enrolamento e no núcleo do transformador. Logo,
A perda no núcleo é a potência que medimos no ensaio de circuito aberto:
Logo, as perdas totais são:
Então, a potência de entrada será:
Logo, o rendimento do sistema será:
Passo 10
Na letra , temos que fazer o mesmo que fizemos para letra , só que agora o fator de potência é capacitivo.
Então, vamos nessa!
Temos o mesmo circuito:
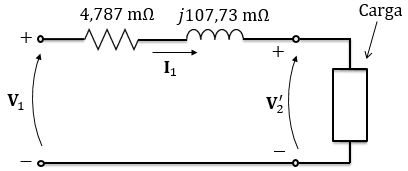
Mas como a carga agora temcapacitivo, o ângulo da corrente irá mudar. Já que
Como o fator de potência é capacitivo o ângulo do fator de potência é negativo, ou seja, . Logo, utilizando a fórmula da potência complexa:
Logo,
Uma outra maneira de se fazer é primeiro calcular o módulo da corrente:
Depois, sabendo que colocamos a tensão na referência e que quando o fator de potência é capacito a corrente está adiantada em relação à tensão, podemos concluir que seu ângulo é positivo.
Passo 11
Aplicando a lei das tensões de Kirchhoff na malha do circuito:
Então, em nosso circuito, quando a carga está ligada, a tensão nos terminais do secundário é igual à tensão que está sendo aplicada na carga. Logo,
Agora, vamos analisar a condição sem carga. Quando não há carga conectada ao secundário, ou seja, quando o transformador está a vazio, temos o circuito abaixo:
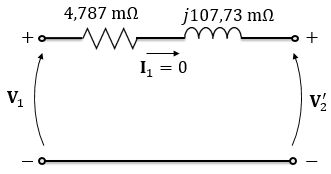
Como o circuito está aberto, não tem circulação de corrente, logo não há queda de tensão nas impedâncias do circuito e toda a tensão aplicada pela fonte conectada no primário é aplicada nos terminais do secundário. Logo,
Então, a regulação de tensão desse sistema será:
Passo 12
O rendimento de um transformador é calculado pela seguinte fórmula:
Em que a potência de entrada é a soma da potência de saída somado com as perdas.
A potência de saída é a potência ativa na carga. Como o fator de potência é a potência ativa será.
Então, como a potência aparente nominal do transformador é .
Já as perdas estão relacionadas às perdas que ocorrem no enrolamento e no núcleo do transformador. Logo,
A perda no núcleo é a potência que medimos no ensaio de circuito aberto:
Logo, as perdas totais são:
Então, a potência de entrada será:
Logo, o rendimento do sistema será:
Resposta