Um transformador de e tem uma reatância de magnetização (quando medida nos terminais de ) de . O enrolamento de tem uma reatância de dispersão de , e o enrolamento de tem uma reatância de dispersão de .
Com o secundário em aberto e aplicados ao enrolamento do primário , calcule a corrente de primário e a tensão de secundário.
Com o secundário curto-circuitado, calcule a tensão de primário da qual resulta a corrente nominal no enrolamento do primário. Calcule a corrente correspondente no enrolamento do primário.
Passo 1
De acordo com enunciado, podemos desenhar o seguinte modelo para esse transformador:
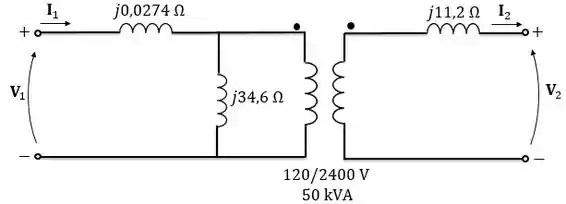
Como nada foi dito sobre as resistências desse transformador, vamos desconsiderá-las.
Passo 2
Para a letra , vamos aplicar no primário e deixar o secundário aberto. Para facilitar o cálculo, vamos usar o modelo referido ao primário do transformador.
Refletindo a reatância do secundário para o primário, temos:
Então, agora que todas as impedâncias estão referidas ao primário, vamos desenhar o modelo :
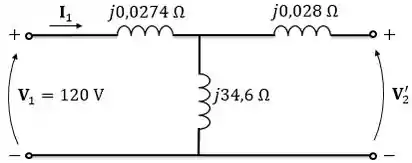
Como o secundário está aberto, a corrente circula apenas pelo primário. Logo, a corrente do primário será:
Passo 3
Já a tensão do secundário refletida é aquela aplicada na reatância de magnetização. Então, aplicando divisor de tensão:
Agora temos que usar a relação de transformação para encontrar a tensão de circuito aberto no secundário.
Passo 4
Na letra , o secundário é curto circuitado:
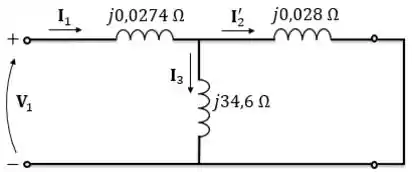
Temos que calcular que resulta com seu valor nominal. O valor nominal de é calculado utilizando os valores de potência aparente e tensão nominal do primário.
Aplicando a lei das tensões de Kirchhoff na malha da esquerda:
Passo 5
Para encontrarmos , temos que determinar antes. Usando divisor de corrente:
Calculando a tensão do primário: