A fórmula computacional para a equação generalizada para o fator de compressibilidade de um gás é dada por
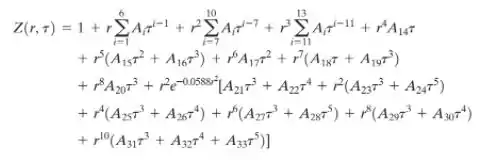
onde , , é a constante do gás em , é a temperatura em , é a pressão em , é o inverso da densidade em , e são a temperatura e a pressão críticas, respectivamente, e os valores das 33 constantes são dados na tabela abaixo e podem ser recuperadas nesta planilha.

Baixe a planilha e no, MATLAB, crie uma função que calcula . Confira sua função, usando , com os seguintes valores de teste:
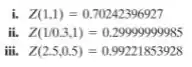
Passo 1
Este exercício é para praticar a função do MATLAB. Os valores das constantes para calcular o fator de compressibilidade , apresentados na tabela do enunciado, estão na planilha abaixo (que você pode acessar e baixar pelo link do enunciado):
A partir dos valores da planilha, você deve construir uma função para calcular e verificá-la com os três valores de teste do enunciado.
Passo 2
Antes de usar o MATLAB, salve a planilha em seu computador indo em:
O print abaixo mostra onde você deve clicar para fazer o download.
Se você não alterar o nome do arquivo, ele ficará salvo como “constantes.xls”.
Passo 3
Em um script novo do MATLAB, crie uma função para calcular . Eu chamei a minha função de , mas você pode chamar como quiser. Esta função deve ter duas entradas, e , a partir das quais ela calcula o fator de compressibilidade :

Por isso, a minha função tem duas entradas, e , e uma saída , que é calculada a partir da equação fornecida pelo enunciado.
A função que calcula deve ser salva na mesma pasta onde você salvou a planilha em Excel, pois é na função que você carregará os dados de “constantes.xls”. Para isto, digite o seguinte comando na função:

O comando carrega a planilha Excel de nome “constantes.xls” no MATLAB. Lembre de adaptar o comando ao nome da sua planilha, caso você tenha nomeado o arquivo de outra forma.
A função vai criar uma matriz chamada , contendo os valores numéricos da planilha, e uma matriz de células chamada , contendo o cabeçalho da planilha. A matriz será uma matriz de linhas, cada uma correspondendo a uma constante , e colunas, sendo que a primeira coluna contém os índices e a segunda coluna, as constantes .
Passo 4
Após incluirmos o comando para carregar a planilha no MATLAB, vamos criar dois vetores, um contendo a coluna de índices e outro com as constantes, com as seguintes linhas de código:
![]()
Na primeira linha de código, eu crio um vetor chamado que contém a primeira coluna da matriz . Logo, o vetor é composto pelos índices da tabela do enunciado e vai de a .
Na segunda linha de código, eu crio um vetor que corresponde à segunda coluna de , sendo composto pelas constantes da tabela do enunciado, indo de a .
Passo 5
O próximo passo é implementar em a equação dada pelo enunciado. Para isso, expanda os somatórios e substitua as constantes , , ... por . Isso quer dizer que, por exemplo, que a constante da equação corresponde ao primeiro elemento do vetor , a constante ao segundo elemento de , e assim por diante.
Substitua também o dos expoentes dos somatórios pelos índices do vetor correspondente. Por exemplo, no primeiro somatório, temos . Em , usaremos , ou seja, . Para o expoente, substituiremos por , logo, o termo do primeiro somatório correspondendo a ficará com essa cara na nossa implementação no MATLAB:
Lembrando que a entrada de corresponde à letra grega .
Considerando tudo isso, é para a equação que calcula fique com essa cara na sua função:

Eu usei os ... para quebrar a linha de código e ficar mais fácil de ver se eu digitei a equação certinho, recomendo que você faça o mesmo =)
Passo 6
Devemos verificar nossa função para três valores de teste, mudando o formato dos números do MATLAB com o comando :
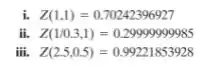
Para isto, usaremos o Command Window. Digite no Command Window o comando e, em seguida, calcule com a função que você criou, considerando e :
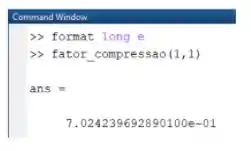
Pelo enunciado, temos que e com nossa função encontramos que , uma diferença de . Por enquanto, nossa função tá com uma precisão bem boa =)
Vamos testar agora , tendo como entrada da função e :
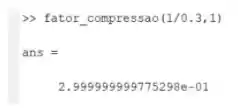
Pelo enunciado, temos que e com nossa função encontramos que , uma diferença de . Outro resultado muito bom!
Finalmente, vamos testar , tendo como entrada de e :

Pelo enunciado, temos que e com nossa função encontramos que , uma diferença de .
As diferenças entre os valores de teste e as respostas de nossa função são apenas residuais, por isso, podemos considerar que nossa função tá show!
Resposta
Ei, a resposta está no passo a passo :)