Taguchi define que o fator de perda médio de um processo é proporcional a
Onde é o desvio padrão, é a média aritmética e é média alvo. Ou seja, ao comparar dois processos, aquele cuja média é mais próxima a e cuja variância é menor é o processo com o menor fator de perda. Copie os dados da tabela abaixo para um arquivo de texto e, com o MATLAB, determine qual processo tem o menor fator de perda médio quando .
Passo 1
Neste exercício, vamos praticar a função do MATLAB. Primeiro, vamos criar um arquivo de texto com a tabela do enunciado. Em seguida, vamos carregar esse arquivo de texto no MATLAB para podermos manipular os dados. Vamos implementar a equação para calcular no mesmo script onde carregamos o arquivo .txt e usar os dados do arquivo de texto para calcular para cada processo. Segundo o enunciado, o que tiver o menor é o que tem o menor fator de perda.
Passo 2
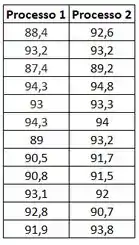
A primeira etapa do exercício consiste em passar os dados da tabela para o Bloco de Notas, como no print abaixo:

Lembre de somente passar para o bloco de notas os valores numéricos, pois quando um arquivo de texto é carregado no MATLAB com a função , ele transforma os dados em uma matriz. Também não se esqueça de trocar as vírgulas por pontos para marcar os decimais.
Após copiar os dados, salve o arquivo em formato .txt. Eu salvei o meu arquivo com o nome “processos.txt”, mas você pode chamar como quiser.
Passo 3
Para carregar o arquivo .txt no MATLAB, usaremos a função . No MATLAB, crie um script novo e salve-o na pasta onde você salvou seu arquivo .txt. Então, digite no script o seguinte comando:
![]()
Com esse comando, vamos carregar no MATLAB os valores numéricos do arquivo de texto “processos.txt”. Lembre de adaptar o comando caso você tenha dado um nome diferente para seu arquivo de texto.
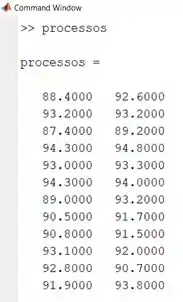
O comando acima armazena os dados do arquivo de texto em uma matriz, cujo nome será o nome do arquivo sem a terminação. No meu caso, será criada uma matriz chamada . Lembre que a sua matriz pode ter um nome diferente, caso você tenha chamado seu arquivo .txt com um nome diferente.
Podemos ver como ficou a matriz que o MATLAB criou rodando o script e imprimindo no Command Window, como no print abaixo:
Passo 4
Para responder a questão, vamos criar dois vetores, um para cada coluna da matriz. Desta forma, ficará mais fácil de calcular o de cada processo.
Para transformar as colunas da matriz em vetores, digite as seguintes linhas de código no nosso script:
![]()
Na primeira linha, armazenamos a primeira coluna da matriz na variável . Logo, é um vetor que contém os dados do Processo 1.
Na segunda linha, fazemos a mesma coisa para o Processo 2: armazenamos a segunda coluna de na variável , logo, é um vetor com os dados do Processo 2.
Passo 5
Vamos calcular para cada processo usando os vetores e . Lembrando que é calculado por:
O enunciado nos dá . O desvio padrão será calculado para cada vetor usando a função do MATLAB, que retorna o desvio padrão de um conjunto de dados. Já a média será calculada aplicando a função em cada vetor, pois ela nos retorna a média aritmética de um conjunto de dados.
Portanto, para calcular o de cada processo, digite em seu script as seguintes linhas de código:

Na primeira linha, definimos a variável , representando a média alvo, e a fazemos igual a , conforme pedido pelo enunciado.
Na segunda linha, calculamos o do Processo 1, cujo resultado é armazenado na variável . Note que aplicamos e no vetor para determinar , pois é o vetor que tem os dados do Processo 1.
Fazemos a mesma coisa para o Processo 2 na terceira linha, onde calculamos do Processo 2, que é armazenado em , usando o vetor .
Para ver o resultado e avaliar qual dos dois processos tem o menor fator de perda média, execute o programa e imprima no Command Window e :

Resposta
O Processo 1 tem e o Processo 2, . O processo que tem o menor fator de perda médio quando é o Processo 2, pois seu é menor.