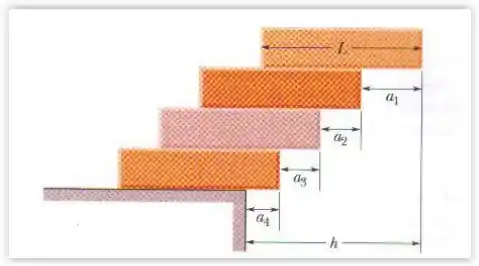
Quatro tijolos de comprimento L, idênticos e uniformes, são empilhados (figura abaixo) de tal forma que parte de cada um se estende além da superfície na qual está apoiado. Determine, em termos de L, os valores máximos para que a pilha esteja em equilíbrio de:
Passo 1
Vamos analisar, primeiramente, .
O centro de massa do bloco mais de cima é , já que ele é uniforme. Logo, percebemos que o valor máximo pode ter é .
Perceba que se for maior que , o peso do bloco concentrado em seu centro de massa fará o bloco de cima girar no sentido horário.
Passo 2
Agora, vamos analisar o .
A situação é a seguinte:
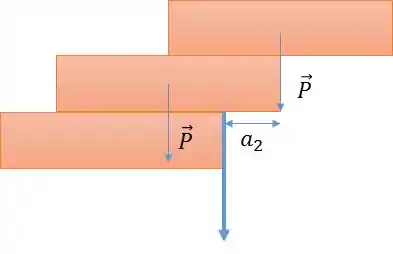
Perceba que o máximo vai ser obtido quando a força concentrada dos pesos do bloco de cima e do bloco do meio atuar no eixo de rotação.
Repare que, se a situação fosse a essa:
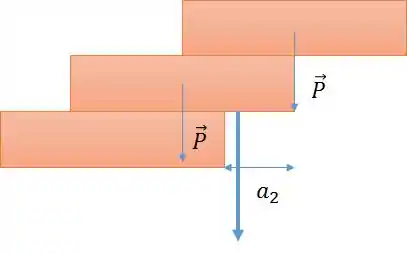
A força concentrada dos dois blocos causaria uma rotação, e os blocos não estariam em equilíbrio.
=
Logo, precisamos saber qual o ponto dessa força concentrada.
Como as duas forças são iguais, vai estar na metade da distância entre as duas.
Passo 3
Mantendo a lógica, devemos achar o ponto em que as forças dos três blocos estão concentradas.
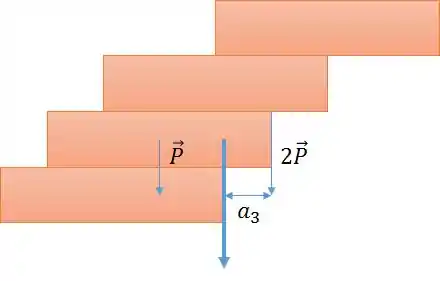
Para descobrirmos esse ponto, devemos calcular o centro de massa dos três blocos.
Podemos definir o eixo passando pela força com seu eixo x positivo orientado para a esquerda e aplicar a fórmula de centro de massa:
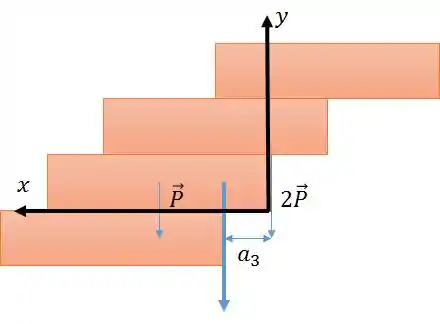
Agora, aplicamos a fórmula de centro de massa.
, sendo a massa de cada tijolo.
O momento gerado por é nulo, já que passa pelo eixo.
Resta então o momento de :
Como é o centro de massa dos três blocos de cima, . Perceba que se fosse maior que isso, a força concentrada dos três blocos estaria à direita do eixo de rotação e geraria torque nos blocos.
Passo 4
d) Para achar o raciocínio é o mesmo. Vamos achar o centro de massa dos 4 blocos juntos e já sabemos que o máximo vai ser o ponto em que a força concentrada dos quatro blocos atua.
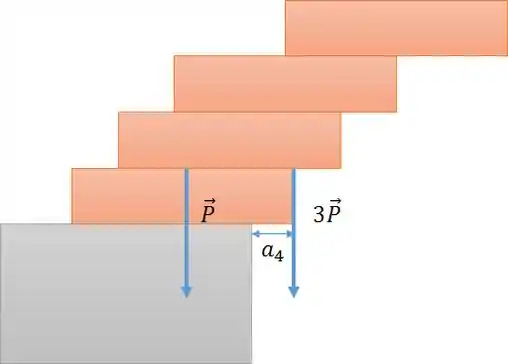
Para aplicar a fórmula do centro de massa, vamos definir o eixo de rotação no ponto onde atua a força com seu eixo x positivo orientado para a esquerda:
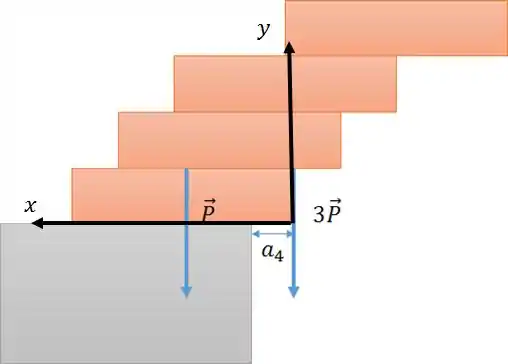
Aplicamos, então, a fórmula de centro de massa:
, sendo a massa de cada tijolo.
O momento gerado por é nulo, já que passa pelo eixo.
Resta então o momento de :
Como o centro de massa é no ponto , o valor máximo de é .
Perceba que se fosse maior que isso, a força concentrada dos quatro blocos estaria à direita do eixo de rotação e geraria torque nos blocos.
Passo 5
máximo vai ser igual a soma de .