Quatro tijolos iguais e uniformes, de comprimento L, estão empilhados em uma mesa de duas formas como mostra a figura abaixo. Estamos interessados em maximizar a distância nas duas configurações. Determine as distâncias ótimas , , e e calcule para os dois arranjos.
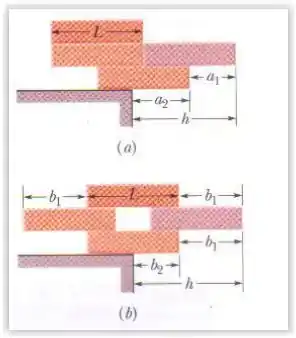
Passo 1
Vamos analisar primeiro o valor de .
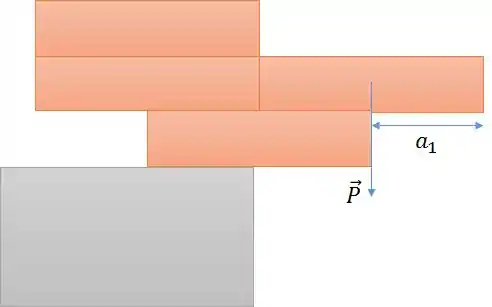
Percebemos que o valor máximo de é no ponto em que o centro de massa do bloco da direita corta o eixo de rotação.
Repare que se fosse maior do que isso, os blocos não ficariam em equilíbrio e tenderiam a rotacionar.
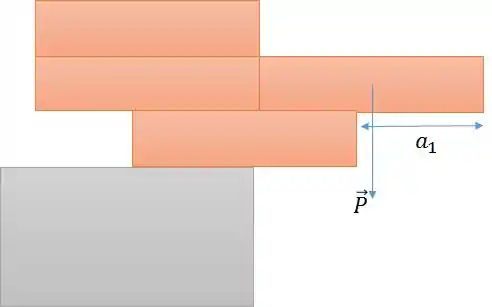
Logo, precisamos saber o centro de massa do bloco da direita. Como é um bloco uniforme, seu centro de massa é .
Passo 2
Vamos analisar o agora.
A situação é a seguinte
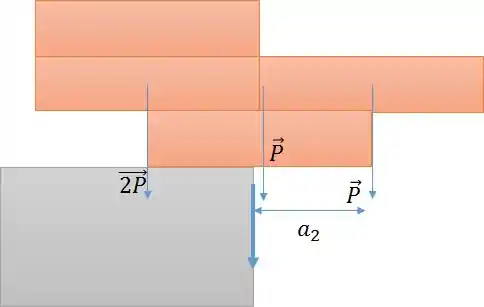
Como no item anterior, precisamos achar o centro de massa dos quatro blocos juntos para descobrirmos o valor máximo de .
Podemos definir o eixo passando pela força do bloco da direita com seu eixo x positivo orientado para a esquerda.
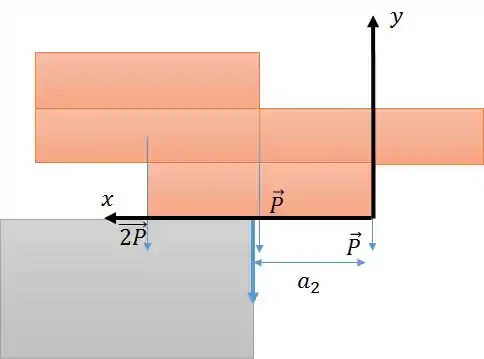
Podemos agora aplicar a fórmula de centro de massa.
, sendo a massa de cada tijolo.
O momento gerado por da direita é nulo, já que passa pelo eixo.
Resta então o momento de e o momento do bloco do meio
Como é o centro de massa dos quatro blocos de cima, . Perceba que se fosse maior que isso, a força concentrada dos quatro blocos estaria à direita do eixo de rotação e geraria torque nos blocos.
Passo 3
para o caso 1 será dado pela soma de com
Passo 4
Vamos analisar agora a situação b. Seguiremos a mesma lógica apresentada anteriormente.
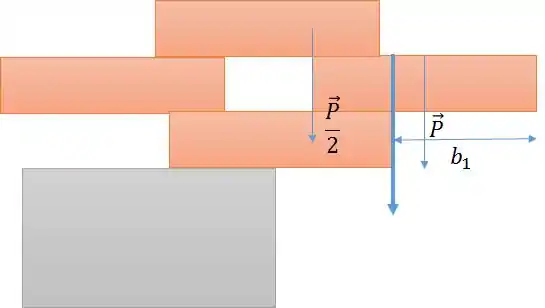
Como é simétrico, podemos achar o centro de massa dos dois blocos da direita e assim descobrirmos o valor máximo de .
Dividimos o peso do bloco do topo em duas forças para baixo, que na situação extrema se encontram na quina dos blocos do meio com valor de como mostra a figura. Repare que é a situação em que o centro de massa será mais distante da extremidade direita, o que nos dará o máximo.
Agora, precisamos achar o ponto de centro de massa dos dois blocos.
Podemos definir o eixo passando pela extremidade do bloco da direita com seu eixo x positivo orientado para a esquerda.
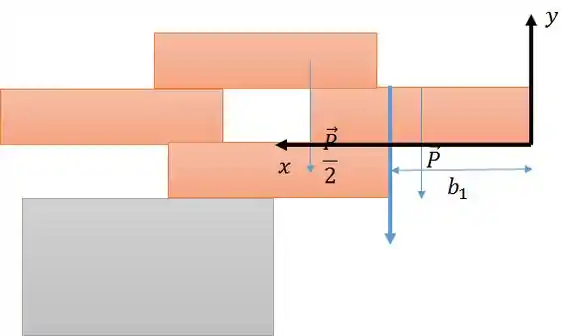
Podemos agora aplicar a fórmula de centro de massa.
, sendo a massa de cada tijolo.
Resta então o momento de e o momento do bloco da direita
Como é o centro de massa dos dois blocos (de cima e da direita), . Perceba que se fosse maior que isso, a força concentrada dos dois blocos estaria à direita do eixo de rotação e geraria torque nos blocos.
Passo 5
Vamos analisar agora .
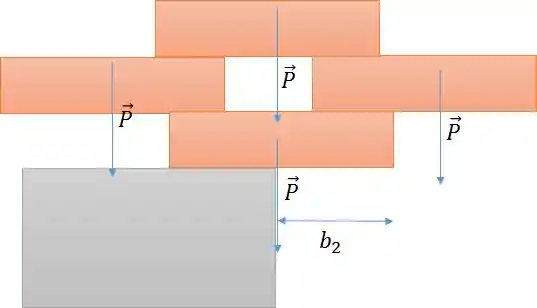
Precisamos, da mesma forma, achar o ponto do centro de massa do quatro blocos juntos. Esse será o valor máximo de .
Pela simetria, é possível perceber que o centro de massa passa justamente no meio do bloco de baixo. Logo, .
Perceba que se fosse maior, os blocos tenderiam a girar para o lado direito e não estaria em equilíbrio estático.
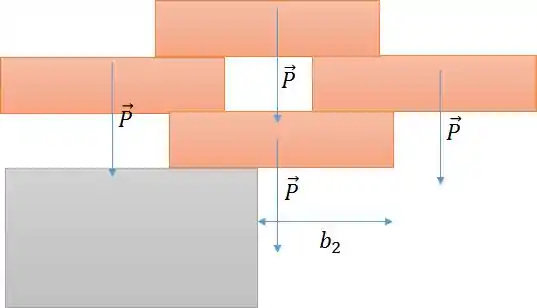
Logo, o valor máximo de é justamente .
Passo 6
Falta agora só calcular que é a soma de e .