Utilize equações de conservação para descrever o movimento de uma partícula confinada em um recipiente em rotação. Considere que o campo centrífugo é bem maior do que o campo gravitacional e que a velocidade angular do recipiente é constante.
Passo 1
É a mesma coisa do exercício anterior, mas agora temos que usar equações de conservação para chegar nas mesmas conclusões.
O enunciado fala pra considerar que campo centrífugo é bem maior do que o campo gravitacional, daí, é como se o campo gravitacional nem existisse, podemos desprezá-lo. E, pela geometria do problema, é conveniente utilizar coordenadas cilíndricas.
Lembrando as componentes de e :
Repara que eu ignorei as componentes em Z porque sabemos que não há nenhuma força motriz para movimento nesse eixo.
Como o enunciado pede pra usarmos equação de conservação, vamos usar a equação do movimento:
E como há movimento em dois eixos, vamos ter que avaliar essa equação para cada um dos eixos.
Para o movimento angular:
Já para o movimento na direção radial, do campo:
Passo 2
Desprezando a fase transiente do movimento (já que é muito rápida), podemos cortar as derivadas no tempo.
Além disso, sabemos que o campo centrífugo é apenas radial então podemos dizer que:
E, considerando que o movimento do fluido é unidirecional, apenas angular:
Dessa forma, as equações ficam:
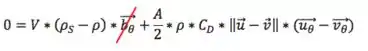
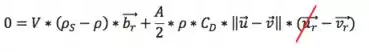
Da primeira tiramos que , ou seja, na direção do movimento do fluido, a partícula se move com a mesma velocidade que o fluido. Uma parte do movimento já provamos.
Para avaliar a segunda, precisamos do valor de :
Voltando com isso pra equação do movimento no eixo radial:
Já igualei essa raiz à velocidade terminal pois, como vimos, essa é a expressão para
velocidade terminal com campo centrífugo, . Ou seja, achamos que na direção do campo:
Resposta
Ei, a resposta está no passo a passo :)