João escreveu uma expressão onde quando , e quando . A expressão ficou dessa forma:
Sabendo que e são variáveis do tipo double responda:
Demonstre a ordem que as expressões serão executadas.
Mostre que quando .
Mostre que quando .
Passo 1
Vamos lá. Essa é uma questão de precedência e associatividade. Então vamos tirar um tempinho pra lembrar da nossa tabela:
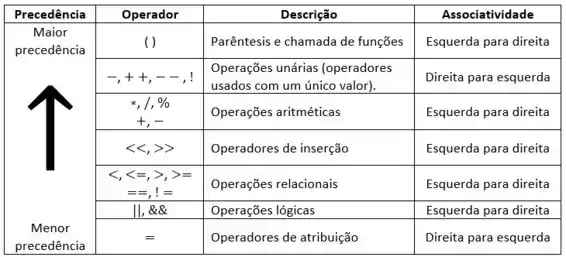
Passo 2
A gente sempre deve começar pelos parêntesis mais internos. Nesse caso é a expressão destacada em vermelho:
![]()
Agora temos 4 parêntesis externos. Todos tem a mesma precedência, mas pela regra de associatividade devemos analisá-los da esquerda para direita
![]()
Depois que os parêntesis estão resolvidos, temos que calcular as multiplicações. Temos duas multiplicações, então, pelas regras de associatividade, devemos analisar da esquerda pra direita.
![]()
Depois é calculada a soma:
![]()
E por fim o valor resultado é guardado na variável :
![]()
Passo 3
Belezinha. Agora vem comigo que vamos colocar essa sequência de passos em prática
Primeiro, onde tiver vamos substituir por :
Em seguida, vamos resolvemos o parêntese mais interno:
Na sequência, resolvemos os parêntesis externos
A gente sabe que e , vamos substituir:
Agora vamos resolver as multiplicações:
E por fim a soma:
Passo 4
Legal né?!
Vamos fazer o mesmo passo a passo, mas para
Primeiro resolvemos o parêntese mais interno:
Agora os parêntesis externos
Sabemos que e , então vamos substituir:
Agora vamos resolver as multiplicações:
E por fim a soma:
Resposta
Ei, a resposta está no passo a passo :)