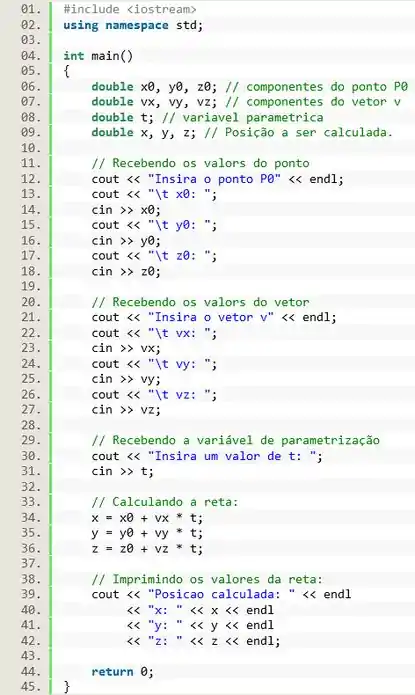
Para saber a equação de uma reta precisamos ter um ponto inicial e um vetor diretor . Com o ponto inicial e o vetor diretor, a equação da reta é dada por:
Onde é uma variável de parametrização.
Conhecendo o ponto e o vetor é possível calcular a posição da reta para qualquer valor de .
Receba do usuário o ponto , o vetor e um valor de , e calcule a imprima a .
Passo 1
E aí pessoal. Aqui é o Juan do Responde Aí, e vamos lá resolver esse exercício.
A questão tem um enunciado bem grande, mas é só porque ela explica pra gente como calcular a equação de uma reta. Na prática, só o que a gente precisa fazer é receber as componentes do ponto, do vetor e o valor de e calcular a reta usando o sistema de equações.
Mas pra começar, a gente precisa escrever o cabeçalho do programa:
![]()
Também precisamos declarar as variáveis do programa. O ponto é composto por três números (suas componentes). Então para receber esse ponto vamos precisar de três variáveis, uma pra cada componente: e , todas do tipo para termos alta precisão de cálculo.
![]()
Seguindo o mesmo princípio, vamos declarar o vetor , que também é composto por outros três números: , e . Elas também serão do tipo
![]()
Já a variável é um valor escalar. Então só precisamos receber o valor de normalmente:
![]()
Certo, já temos tudo que precisamos para calcular a reta! Porém precisaremos de variáveis para guardar esses resultados. Então vamos criar as variáveis , e para armazenar os resultados. Note que essas variáveis devem ser do tipo , pois todas as demais variáveis da equação são deste tipo também:
![]()
Passo 2
Show de bola! Temos as variáveis todas declaradas, então precisamos preencher as variáveis com os valores do usuário. Para isso vamos usar o para solicitar os valores, e o para armazenar cada valor na variável adequada
Primeiro, na linha 12, vamos exibir uma mensagem informado qual item vamos receber. Eu vou querer receber primeiro o ponto . Em seguida, na linha 13, vou informar para o usuário que quero receber a componente . Note que coloquei uma tabulação para facilitar a visualização. E na linha 14 usamos o comando para guardar o valor digitado na variável . E vamos repetir o mesmo processo nas linhas 15 a 19 para receber as demais componentes do ponto :
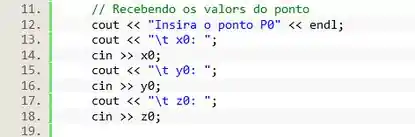
Seguindo a mesma lógica, vamos receber também os valores do vetor e armazenar nas variáveis , e .

E também vamos receber um valor para a variável paramétrica :

Belezinha!
Passo 3
Ok, agora que temos todos os valores, podemos calcular o valor da reta. Pra isso, vamos precisar montar as seguintes equações:
Vamos usar o operador de multiplicação () e o operador de adição () para escrever a equação e com o operador de atribuição () guardamos na variável adequada.
A precedência maior é do operador de multiplicação, depois do de soma e por último do operador de atribuição. Então, nesse caso não vamos precisar utilizar parêntesis:
![]()
E fazemos o mesmo para calcular e :
![]()
Passo 4
Agora a questão ta quase concluída. Só precisamos exibir o resultado, e pra isso vamos usar o .
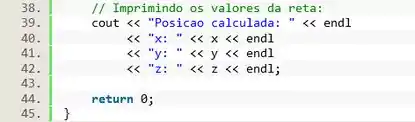
Passo 5
Para testar se o programa funciona direitinho, vamos rodar ele com os seguintes valores
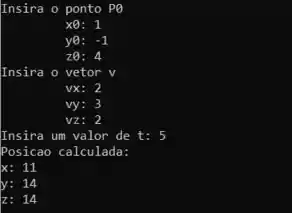
E rodou liso que nem manteiga! Deu tudo certo, questão concluída!
Resposta