Condução de Calor Multidimensional
Teoria
Introdução
Quando estamos analisando a condução de calor, temos, basicamente, dois objetivos:
- Determinar a distribuição de temperaturas;
- Determinar o fluxo térmico.
Ao olharmos pra uma situação desse tipo:
Onde , é de boa saber que o calor é transferido da esquerda para a direita. Além disso, com um pouco mais de informação, podemos determinar, inclusive a forma como o calor está distribuído.
No que estamos interessados agora é em situações com essa cara aqui:
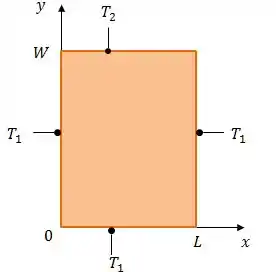
Onde, novamente, . Repare que, agora, somo somente uma superfície possui temperatura maior que as outras, o calor não vai ser mais transferido unidimensionalmente.
E agora, José?!
Pra entender como faremos pra sair dessa roubada, vamos olhar para a equação de calor, dada por:
Vamos fazer aqui as seguintes considerações:
- Condução bidimensional (em e );
- Regime estacionário ();
- Não há geração de energia ();
- Condutividade térmica constante.
Aplicando essas simplificações, teremos o seguinte:
Pra facilitar a análise, vamos definir uma temperatura adimensional, dada por:
Assim, para e para . Assim, a equação de calor fica resumida a:
Onde as condições de contorno são definidas por:
“Beleza, mas como resolvemos essa equação diferencial?!”
Nesse tipo de casos, é válido usarmos um método chamado método da separação de variáveis. A ideia dele é basicamente a seguinte: vamos dizer que a função é, na verdade, o produto de duas funções independentes e . Dessa forma:
Substituindo essa expressão na nossa equação de calor e arrumando a casa, encontraremos isso:
Pra conseguirmos resolver esses caras separadamente, vamos igualar os dois lados da expressão a uma constante de separação . Assim, teremos:
Opa! Essas são equações que sabemos resolver! :D Essas lindezas possuem as seguintes soluções:
Assim, o nosso é dado por:
Pra determinar as constantes , e basta aplicar as condições de contorno.
Aplicando as condições de contorno.
Para cada condição, teremos os seguintes resultados:
- .
- .
- :
Onde Assim:
Substituindo isso tudo na expressão de , teremos:
Ainda podemos usar a notação de Euler para os termos exponenciais:
Combinando as constantes e e admitindo que elas possam depender de , podemos escrever a temperatura adimensional como sendo:
Na real a constante é dada por:
“Show de bola, mas então a temperatura fica em função de ?”
Na verdade, a temperatura será dada pela seguinte forma:
Tá, pode ser que você esteja mais ou menos assim agora:
Mas CALMA, podemos partir direto dessa série pra resolver a maior parte dos problemas. Vamos ver isso nos exercícios?
E agora, José?!
Aplicando as condições de contorno.
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Uma placa retangular bidimensional está sujeita às condições de contorno especificadas.
Usando os resultados da solução exata para a equação do calor apresentados na teoria, calcule a temperatura no ponto central , utilizando os cinco primeiros termos não-nulos da série infinita que deve ser determinada.
Passo 1
A distribuição de temperatura é dada por:
Onde e . Como estamos considerando o ponto e , vamos começar substituindo os valores pra ver se conseguimos simplificar a equação:
Passo 2
Para qualquer valor par de , o termo será nulo. Dessa forma, como estamos preocupados em pegar os 5 primeiros termos da série, vamos utilizar os seguintes valores de :
Assim, pegando os 5 primeiros termos da série, teremos:
Jogando isso tudo na calculadora, teremos:
Passo 3
A temperatura central será:
Substituindo os valores:
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Considere que a placa retangular bidimensional abaixo possua uma condutividade térmica de .
Partindo da solução exata para a distribuição de temperaturas, deduza uma expressão para a taxa de transferência de calor, por unidade de espessura, saindo pela superfície inferior da placa.
Calcule a taxa de transferência de calor considerando os cinco primeiros termos não-nulos da série infinita.
Passo 1
Sabendo que o fluxo térmico muda ao longo de , e que o calor está sendo transferido para fora da placa, o mesmo pode ser calculado da seguinte forma:
Utilizando a relação entre e , temos que:
Assim:
Show de bola! Já sabemos do que precisamos pra chegar à expressão da taxa de transferência de calor.
Passo 2
Sabemos que é dado por:
Pra derivar em relação a , precisamos lembrar que a derivada do é o dessa função. Aí, aplicando a regra da cadeia ali naquele :
Igualando a 0:
Agora podemos seguir com a brincadeira.
Passo 3
Substituindo na expressão da taxa de transferência de calor:
Agora é ir arrumando a bagunça:
Onde e . Assim:
Passo 4
Ok! Queremos trabalhar com os 5 primeiros termos da série, mas repare que, para qualquer valor par de , a série será nula. Assim, vamos considerar os seguintes valores:
Calculando o somatório para cada um dos valores de :
Logo:
