Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 4.Problemas - Ex. 152
Considere um pedaço cilíndrico de carne de cordeiro de 7,6 cm de comprimento e 3 cm de diâmetro. Quinze pedaços de carne inicialmente a 2°C são colocados em água fervente a 95°C com um coeficiente de transferência de calor de . A quantidade de calor transferido durante os primeiros 8 minutos de cozimento é:
a) 71 kJ;
b) 227 kJ;
c) 238 kJ;
d) 269 kJ;
e) 307 kJ.
Passo 1
Boom galera, muita calma nessa hora !!
Primeiro, nós queremos achar o que?
O calor transferido para a carne, certo?
Para isso vamos usar a equação para uma geometria bidimensional formada pela interseção de duas geometrias unidimensionais, que no caso é uma parede e um cilindro:
Para começo de conversa vamos achar , olhando a fórmula:
Se:
Agora só precisamos da massa, mas isso é moleza!! Vamos usar a densidade:
Por ser um cilindro:
Como:
Então:
Achando o calor máximo:
Passo 2
Agora nós precisamos achar as transferências de calor fracionárias para as diferentes geometrias, não é?
Começando pela parede:
Para calcular nós precisamos achar o número de Biot:
Sabemos que:
Agora é só calcular o Biot:
Olhando a Tabela:
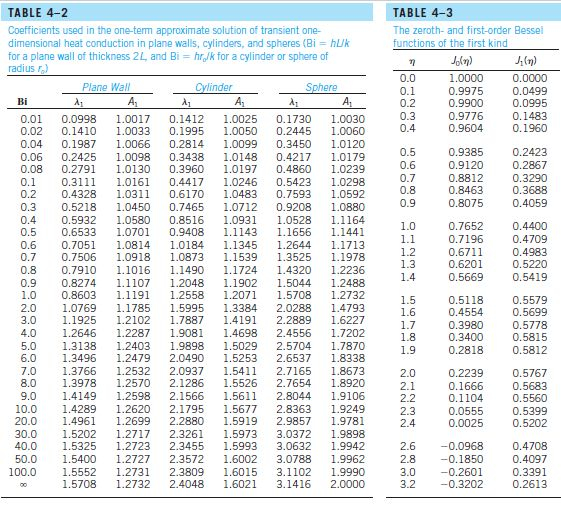
Nós vemos que:
Com estes dados nós conseguimos achar outro termo, o
Só precisamos do tempo adimensional, se lembram como?
Temos que:
Agora é só calcular:
Agora temos tudo o que precisamos, não é mesmo?
E quando você acha que acabou, acabou foi nadaaa!!!
Nós precisamos do calor, não é?
Então é só substituir:
Passo 3
Agora nós precisamos do calor fracionário do cilindro:
Para calcular nós precisamos achar o número de Biot:
Sabemos que:
Agora é só calcular o Biot:
Olhando a Tabela:
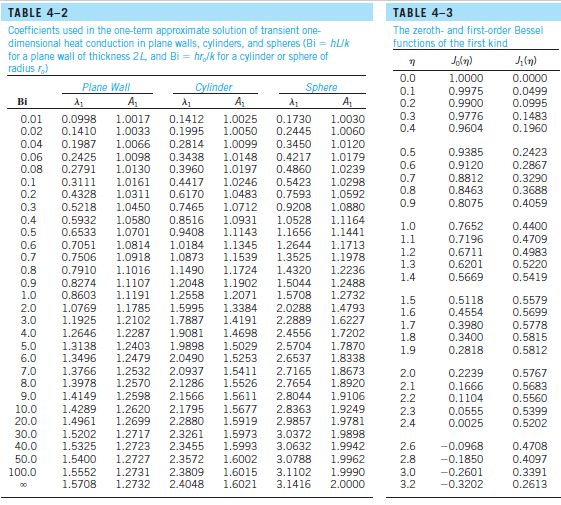
Como não temos o valor de Biot nós precisamos interpolar:
Usando os dados para um cilindro:
Substituindo:
Com entes dados nós podemos calcular mais um termo:
Maaais uma interpolação:
Usando:
Calculando:
Com estes dados nós conseguimos achar outro termo, o
Só precisamos do tempo adimensional, se lembram como?
Temos que:
Agora é só calcular:
Agora temos tudo o que precisamos, não é mesmo?
No calor:
Passo 4
Se temos todos os dados só nos resta colocar na fórmula do Passo 1:
Ou melhor:
Achando o calor:
O mais próximo no nossa caso:
Galerinha, foi um pouco distante, não é? Mas é isso aí !