Análise Dimensional
Teoria
E aí? Belezinha? Lembra desse nome análise dimensional? Sabe quando a gente vê a unidade de todos os termos das nossas equações… Então, quando a gente torna algum termo adimensional é como se a gente tirasse aquela unidade… estranho?
Vamos de exemplo que dá aquela facilitada no entendimento! Sabe o número de fourier? Então ele pode é um parâmetro adimensional, ou seja, não tem unidade! Mas olha só como vemos isso:
Pra achar ele precisamos da difusividade térmica (), m²/s, do tempo, s, e do comprimento onde ocorre a difusão, m. Colocando nossas unidades na equação vemos que elas vão se cortar e por conta disso o número de Fourier é adimensional!
Viu só? Show de bolinhas!
Análise dimensional de transferência de massa convectiva
Se a gente considerar a transferência de massa da parede de um tubo para o fluido escoando através do conduíte, podemos fazer a seguinte análise, vem comigo!
Vamos fazer uma tabela com as variáveis que usamos, nessas condições, o símbolo delas e a unidade de cada uma, olha só:
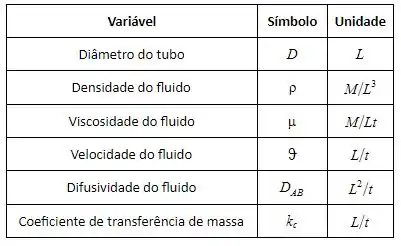
Muito termos! Mas relaxa que vamos conseguir adimensionalizar essa galera, sabe como? Usando matriz! Pra começar a gente vê que existem fatores comuns, olha só, basicamente para representar a unidade de todo mundo levamos em consideração a massa, litro e tempo, certo?
Essas vão ser as linhas da nossa matriz! E as colunas serão nossos símbolos… Vamos colocar o número de vezes que cada um aparece no meio da nossa matriz. Olha só como vai ficar:
Agora que montamos a nossa matriz vamos fazer algumas análises simples. Qual é o rank da nossa matriz, ou seja, o número de linhas não nulas dela, temos que:
rank
Agora, temos um total de variáveis, então podemos descobrir quantos grupos adimensionais temos:
Beleza pura! Temos então grupos adimensionais! E sendo , e variáveis centrais, pois nelas estão todas as nossas dimensões básicas, vamos ter:
Agora escrevendo na forma adimensional, vamos ter:
E isso nos dá:
Pela equação do , já sabemos que , e pela equação do , sabemos que , sendo assim, substituindo na equação de , temos:
Agora descobrimos que para adimensionalizar , precisamos de:
E esse termo em transferência de massa é conhecido como número de Nusselt (Nu) ou número de Sherwood (Sh).
Agora fazendo esse mesmo procedimento para o , temos:
E isso nos diz:
Vamos ficar então com:
E para , teremos:
Opa! Em transferência de massa, esse termo é o número de Schmidt (Sc). E fazendo uma relação entre o e o , encontramos:
E esse aí é o número de Reynolds (Re)! Sendo assim, nossa relação de adimensionalização é dada por:
Análise dimensional de correntes de convecção natural
Quando temos uma parede plana vertical com um fluido adjacente, temos esse caso de uma convecção natural, vamos fazer a mesma análise de antes, ok?
Montando a matriz vamos ficar com:
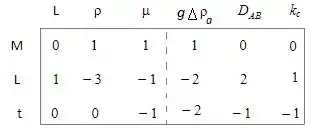
Mais uma vez, nosso ranke nosso total de variáveis, então temos:
Temos grupos adimensionais de novo! E sendo , e as nossas variáveis centrais, vamos ficar com:
Fazendo a adimensionalização de cada um, vamos ficar com:
O nos dá o número de Nusselt (Nu), o nos dá o inverso do número de Schmidt (Sc), agora vamos achar uma relação entre o e o :
Opa! Essa relação nos deu o número de Grashof!
Então nós temos que para uma convecção natural nossa relação de adimensionalização é dada por:
E aí curtiu? Parece complexo, mas depois a gente pega o jeito, né? Então agora partiu fazer uns exercícios e ficar tudinho!
Análise dimensional de correntes de convecção natural
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Qual a importância da análise dimensional na transferência de massa convectiva?
Passo 1
Fala aí! Vamos resolver essa questão juntos!
Bom, nosso enunciado quer saber a importância da análise dimensional…
A análise dimensional é um método para reduzir o número de variáveis de um problema para um conjunto menor de variáveis, e elas não possuem dimensão física, isso simplifica a resolução de problemas complexos da transferência de massa convectiva, bem como em toda parte do estudo de fenômenos de transporte.
Show de bola!
Resposta
Passo 1.
Exercício Resolvido #2
Elaboração própria.
Quais as quatro principais dimensões primárias que são usadas na análise dimensional? Represente duas grandezas usando essas dimensões.
Passo 1
Bom, essa aí é pra fixar nossos conhecimentos com o que vimos na teoria, ok?
Dimensões primárias são aquelas que são bases pra gente fazer a análise dimensional. A gente usa normalmente quatro, que são as principais para representar as unidades dos nossos parâmetros, elas são:
- Tempo
- Comprimento
- Massa
- Temperatura
Passo 2
Bom, agora a gente precisa representar duas grandezas… Humm… Vamos começar representando o coeficiente de difusão mássica , se observarmos a unidade dele costuma ser , isso quer dizer que temos o comprimento ao quadrado dividido pelo tempo, logo, nossa dimensão fica então:
Agora vamos fazer o mesmo para a viscosidade do fluido , ela pode ser representada pela unidade , então a dimensão primária fica:
Prontinho!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria.
Como podemos encontrar o número de grupos adimensionais independentes? Qual será a quantidade de grupos adimensionais para análise das seguintes variáveis: velocidade, viscosidade, diâmetro e densidade?
Passo 1
Nessa aqui vamos começar respondendo como encontramos a quantidade de grupos adimensionais, beleza? É uma formulazinha simples pra ficar na cabeça, ok?
Total de variáveis Número de dimensões primárias
Esse número de dimensões primárias, também é conhecido como rank, então se ver escrito isso já sabe, beleza?
Passo 2
Bom agora que sabemos como calcular, vamos começar separando as dimensões primárias das variáveis dadas no enunciado, olha só:
Velocidade:
Viscosidade:
Diâmetro:
Densidade:
Show! Então vemos que estamos usando variáveis e dimensões primárias, vamos ter então:
Show de bola! Vamos ter um grupo adimensional independente.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração própria.
Como podemos montar a matriz que ajuda a determinar o sistema para descobrir o grupo adimensional? Monte a matriz para as seguintes variáveis: velocidade, viscosidade, diâmetro e densidade?
Passo 1
Se liga só, a matriz nos dá um suporte muito bom pra montar o sistema, mas não precisamos montar ela necessariamente para resolver os problemas de análise dimensional, ok?
Mas aqui precisa porque o enunciado tá pedindo hehe
Bom, temos os seguintes parâmetros e suas dimensões:
Velocidade:
Viscosidade:
Diâmetro:
Densidade:
Para montar a matriz precisamos, na vertical, à esquerda, colocar nossas dimensões primárias… E na horizontal, em cima, colocar o símbolo dos nossos parâmetros: velocidade , viscosidade , diâmetro e densidade , nossa matriz ficará assim, até agora:
M
L
t
No meio da nossa matriz vamos colocar a quantidade de cada uma das dimensões em cada um dos parâmetros, olha só:
M
L
t
Se ligou que quando as dimensões estão no denominador fica negativo, né? Show de bolinhas!
É isso aí!! Montamos a matriz! Arrasamos!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração própria.
Como podemos identificar as variáveis centrais, na análise dimensional?
Passo 1
Opa! Atenção nessa questão que é simples, mas muitoooo importante pra gente fazer uma análise dimensional certinha!
Em todo conjunto de variáveis que forem fornecidos pra gente fazer a análise dimensional, teremos as variáveis centrais…
As variáveis centrais podem ser qualquer uma que inclua todas as dimensões básicas do problema que estivermos trabalhando… A quantidade de variáveis centrais tem que ser igual ao número de grupos adimensionais que vamos ter, pois cada uma ficará em um grupo adimensional…
Ainda não ficou visível, né? Vamos de exemplo então! Se temos:
Então, são variáveis e dimensões, logo teremos grupos adimensionais… Opa! Então serão variáveis centrais, ok?
Elas serão as que mais contém todas as dimensões básicas, então vão ser: a difusividade do fluido, a densidade do fluido e o diâmetro do tubo!
Prontinho! Só precisaremos disso se o problema não disser pra gente os parâmetros repetidos, ok?
Show de bolinhas!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Universidade Federal do Pará - Fenômenos de transporte I - Professora Cristiane
Na transferência de massa por convecção forçada as variáveis pertinentes são: massa específica , comprimento característica , difusividade de massa , viscosidade dinâmica , velocidade e coeficiente de transferência de massa . Determine os grupos adimensionais sendo que , e formam o grupo de grandezas repetidas.
Passo 1
Vamos resolver esse probleminha de análise dimensional!
Pra começar vamos separar as variáveis e suas dimensões, ok?
Temos então, seis variáveis e três dimensões primárias , logo:
Opa! Então nós vamos ter três grupos adimensionais!
Passo 2
O enunciado já disse pra gente que as grandezas repetidas, serão , e … Então nossos três grupos ficaram assim:
Agora vamos escrever cada um deles em relação às dimensões. Lembrando que nossos coeficientes precisam ser iguais a zero, temos:
Isso nos diz que:
Então temos:
Sendo assim teremos:
Portanto nosso primeiro grupo adimensional será:
Passo 3
Agora vamos fazer o mesmo para o segundo grupo adimensional!
Isso nos diz que:
Então temos:
e
Sendo assim:
Portanto nosso segundo grupo adimensional será:
Passo 4
E para fechar, vamos fazer o mesmo para o terceiro grupo adimensional!
Isso nos diz que:
Então temos:
e
Sendo assim:
Portanto nosso terceiro grupo adimensional será:
Uhul! Finalizamos!
Resposta
Os grupos adimensionais são:
Exercício Resolvido #7
Universidade Federal do Pará - Fenômenos de transporte I - Professora Cristiane
Num processo de galvanização, a velocidade com que os íons se movem em soluções eletrolíticas diluídas para eletrodo em forma de disco, é função da velocidade de difusão de massa dos íons. O processo depende do controle das variáveis abaixo. Obtenha os grupos adimensionais para estas variáveis, onde , e estão cada um em grupos diferentes.
Dados:
coeficiente de transferência de massa
diâmetro do disco
massa específica
coeficiente de difusão
velocidade angular
viscosidade
Passo 1
Vamos fazer essa análise dimensional!
Começando com a separação sas variáveis e suas dimensões, ok?
Temos seis variáveis e três dimensões primárias , então:
Vamos ter três grupos adimensionais!
Passo 2
O enunciado já disse pra gente que as grandezas que não se repetem são: , e … Então elas ficaram cada uma em um grupo, e nossos grupos adimensionais ficaram assim:
Agora vamos escrever cada um deles em relação às dimensões. Lembrando que nossos coeficientes precisam ser iguais a zero, temos:
Isso nos diz que:
Então temos:
Sendo assim teremos:
Portanto nosso primeiro grupo adimensional será:
Passo 3
Agora vamos fazer o mesmo para o segundo grupo adimensional!
Isso nos diz que:
Então temos:
e
Sendo assim:
Portanto nosso segundo grupo adimensional será:
Passo 4
E para fechar, vamos fazer o mesmo para o terceiro grupo adimensional!
Isso nos diz que:
Então temos:
e
Sendo assim:
Portanto nosso terceiro grupo adimensional será:
Uhul! Finalizamos!
Resposta
Os grupos adimensionais são:
Exercício Resolvido #8
Universidade Federal de Pernambuco - Análise dimensional e semelhança - Professor Alvaro
A força de arrasto sobre uma esfera lisa, estacionária, depende de , , e . Obter um conjunto de grupos adimensionais que possam ser usados para correlacionar dados experimentais.
Passo 1
Partiu fazer a análise dimensional para encontrar o conjunto de grupos adimensionais que o exercícios pediu!
Começando com a separação sas variáveis e suas dimensões:
Temos cinco variáveis e três dimensões primárias , então:
Vamos ter dois grupos adimensionais!
Passo 2
Como temos três dimensões primárias, vamos ter três parâmetros repetidos! Vamos escolher, como parâmetro repetido, a massa específica, o diâmetro e a velocidade, ok? Nossos grupos adimensionais, serão:
Agora vamos escrever cada um deles em relação às dimensões. Lembrando que nossos coeficientes precisam ser iguais a zero, temos:
Isso nos diz que:
Então temos:
e
Sendo assim teremos:
Portanto nosso primeiro grupo adimensional será:
Passo 3
Agora vamos fazer o mesmo para o segundo grupo adimensional!
Isso nos diz que:
Então temos:
e
Sendo assim:
Portanto nosso segundo grupo adimensional será:
Podemos então tirar a relação funcional, dos dois grupos adimensionais, sendo ela:
Show de bolinhas!
Resposta
Os grupos adimensionais são:
A relação funcional é: