Transferência de massa na camada limite
Produzido por Giovanna RonzéTeoria
Fala aí galera!! Vamos estudar mais um tópico juntos? Com certeza!!
Aqui a gente vai bater um papo sobre transferência de massa na camada limite… Humm… Mas quem é essa tal de camada limite?
Sei que esse nome já apareceu pra gente em outros assuntos, mas não custa dar aquela relembrada, né?
De um modo geral, podemos chamar de camada limite, uma fina camada que se forma na superfície de um sólido por onde escoa um fluido… E é nesta camada estreita que as forças de atrito são muito importantes, pois ela retarda a velocidade externa, do fluido, para um completo repouso na parede.
Essa definição de camada limite, nos mostra duas regiões diferentes, vamos ter um escoamento externo e um escoamento interno. E justamente nessa camada interna é que vamos ter forças viscosas e irrotacionais que não vamos poder desprezar, beleza?
Quando temos um escoamento em uma superfície sólida temos um atrito superficial, que está ligado a Camada Limite de Velocidade, vamos ter também uma transferência de calor, ligada a Camada Limite Térmica e uma transferência de massa convectiva, que está ligada a Camada Limite de Convecção…
Vamos falar de cada uma delas com calma, porque todas elas se relacionam ao coeficiente convectivo, que é muito importante pra gente agora!
Camada Limite de Velocidade
Bom, vamos analisar um escoamento, e esse fluido entra em contato com uma superfície sólida e ele escoa sobre ela, no momento em que se forma um filme na superfície em que as partículas passam a ter velocidade nula.
E essas partículas que ficam com a velocidade zero influenciam no movimento das outras partículas que estão ao lado delas, retardando o movimento delas. E isso será uma reação em cadeia até esse efeito ser desprezível.
Dá uma olhadinha nesse esquema aqui:
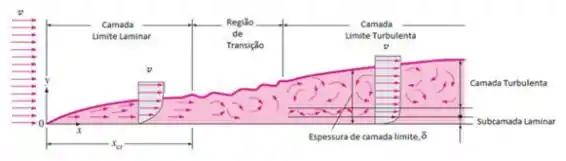
Esse escoamento, tendo uma parte mais rápida e uma parte mais lenta vai levar a uma tensão de cisalhamento proporcional ao gradiente da velocidade:
Esse é a velocidade do fluido que vai variar da superfície, onde , até o limite, onde . E essa distância é a espessura da Camada Limite que vai evoluindo no decorrer no eixo .
Camada Limite Térmica
Essa aqui vai ser bem parecida com a que acabamos de ver… Também temos um fluido escoando sobre uma superfície sólida, mas agora vamos analisar a diferença de temperatura nesse escoamento.
Quando as moléculas, que estão em movimento, entram em contato com a superfície, elas tendem a encontrar o equilíbrio térmico e para isso trocam energia em forma de calor com as outras moléculas sucessivamente… Viu só como é bem parecido com a camada limite da velocidade?
Como temos trocas de calor entre as moléculas, temos um gradiente de temperatura que vai variar entre a temperatura da superfície sólida e a temperatura do fluido. E a região onde ocorre essa variação será a espessura da camada limite térmica … Dá uma olhadinha nesse esquema aqui:
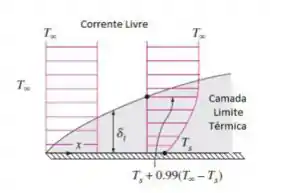
Essa temperatura é a temperatura da corrente livre, beleza?
Pensando no princípio de Fourier, podemos encontrar o fluxo térmico na superfície local, dessa forma:
E como não vamos ter movimento de fluido na superfície teremos a troca de calor acontecendo por condução.
Camada Limite por Convecção
Essa aqui é justamente onde queremos chegar!!! E ela vai ser muito parecida com as outras duas que nós vimos. Aqui também vamos ter um gradiente, mas dessa vez será um gradiente de concentração, que será entre as concentrações sobre a superfície e a do escoamento de uma determinada espécie.
Saca só esse esqueminha aqui:
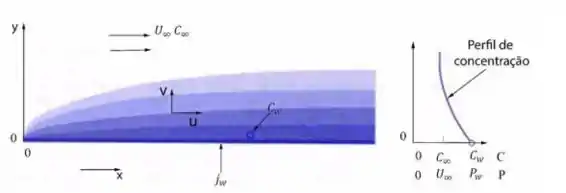
Ele mostra pra gente o desenvolvimento da camada limite para um fluido estando em uma placa plana. E aqui a gente observa o mesmo que nas outras camadas, a concentração na superfície vai influenciando as concentrações seguintes, a partir do momento em que a transferência de massa da espécie vai penetrando na corrente livre.
Vamos definir o fluxo molar na superfície como sendo:
E vamos definir o coeficiente de transferência de massa por convecção como sendo:
A distribuição das concentrações no escoamento será dada pela equação:
E usaremos como condições de contorno:
Será quando
E quando
Utilizando analogias com a transferência de calor, podemos escrever a seguinte relação:
, se
Logo, temos então que o número de Sherwood, pode ser dado como:
, se
E esse é o número de Schmidt que é dado por:
Mais uma vez fazendo analogias com a transferência de calor, vamos ter:
, se
E sendo o coeficiente de transferência de massa dado por:
Vamos ter que o número de Sherwood fica:
Opa! Então teremos o seguinte:
, se
e
, se
Além disso, também podemos ter o coeficiente de transferência de massa, baseado no fluxo de massa… Ele será dado dessa forma aqui:
Muita informação, né? Vamos fazer uns exercícios para fixar melhor tudo isso!

Camada Limite Térmica
Camada Limite por Convecção
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Defina camada limite e cite as três diferentes camadas limites de um escoamento.
Passo 1
Fala aí! Vamos resolver essa questão juntos!
A camada limite é uma camada fina que se forma na superfície de um sólido por onde escoa um fluido. Nessa fina camada atuam forças de atrito que retardam a velocidade de escoamento das moléculas.
Temos três tipos de camada limite, a camada limite de velocidade, camada limite térmica e camada limite convectiva ou de concentração.
Prontinho!! Acabamos esse aqui!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria.
Identifique um problema, na convecção, quanto as camadas limites.
Passo 1
Essa questão aqui tá bem ampla, né? Mas na real ela quer saber qual o problema comum às três camadas limites!
Bom, temos a camada limite de velocidade, a camada limite térmica e a camada limite de convecção, elas apresentam várias semelhanças, vamos dar uma olhadinha num esquema que mostra as três camadas….
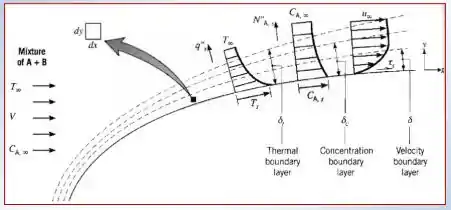
Uma semelhança importante entre elas é que todas dependem de coeficientes de convecção e a determinação desses coeficientes é o problema comum a todas.
Os coeficientes convectivos são funções da geometria da superfície e das condições que está acontecendo o escoamento, além disso eles dependem de algumas propriedades, como densidade, viscosidade, condutividade térmica e calor específico.
Show de bolinhas! Identificamos um problema na convecção.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria.
Construa uma tabela com as analogias entre a transferência de calor e a transferência de massa, no que diz respeito a camada limite por convecção.
Passo 1
E aí belezinha? Então esse exercício tá pedindo pra gente fazer comparações, das equações que usamos na camada limite por convecção, entre a transferência de calor e a transferência de massa… Vamos nessa!
Vamos começar identificando as analogias entre os símbolos, beleza?
Transferência de Calor Transferência de Massa
Passo 2
Agora vamos usar as equações, colocando de um lado as da transferência de calor e do outro as de transferência de massa… Olha só como vai ficar:
Transferência de Calor Transferência de Massa
Prontinho! Arrasamos!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Lista de exercícios sobre convecção mássica.
Por que a espessura da camada limite mássica aumenta com a injeção de matéria? Qual o efeito disso no fluxo de massa?
Passo 1
O exercícios tá perguntando pra gente o porquê da espessura da camada limite aumentar com o aumento de matéria, ok?
Bom, a gente definiu lá na nossa teoria que camada limite é uma fina camada que se forma na superfície de um sólido por onde escoa um fluido, certo? E vimos também que ela retarda a velocidade externa do fluido, né?
Então, nós temos efeitos por conta da inércia e efeitos por conta da velocidade e eles terão a ordem de grandeza, dá só uma olhada:
Sendo assim, a espessura da camada limite pode ser dada por:
Sendo a viscosidade, o comprimento do escoamento, a massa específica do fluido e o a velocidade do escoamento.
Olhando então para essa conclusão, vemos que a espessura da camada limite é diretamente proporcional ao comprimento do escoamento, que por sua vez está ligado a injeção de matéria, tranquilo?
Mas e o efeito disso no nosso fluxo de massa? Bom a gente viu que a transferência de massa por convecção é equivalente ao fluxo molar dividido pelas concentrações do escoamento:
Logo, se a gente aumenta a quantidade de matéria, aumentamos a concentração, então vamos diminuir nosso coeficiente convectivo… Opa! Então isso quer dizer que o aumento de matéria diminui o fuxo de massa convectiva.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
IFRS - Prova de Engenharia Química.
Sobre a camada limite, analise as afirmativas, identificando com “V” as VERDADEIRAS e com “F” as FALSAS, assinalando a seguir a alternativa CORRETA na sequência de cima para baixo.
( ) A camada limite é a região adjacente a uma superfície sólida na qual tensões viscosas estão presentes, em contraposição à corrente livre onde as tensões viscosas são desprezíveis.
( ) As tensões viscosas presentes na camada limite são decorrentes do cisalhamento das camadas do fluido.
( ) Gradientes de velocidade na camada limite originam tensões viscosas nesta região.
( ) Na camada limite laminar existem gradientes de velocidade, os quais não estão presentes na camada turbulenta.
( ) A espessura da camada limite pode ser definida como sendo a distância da superfície na qual a velocidade situa-se dentro de 1% da velocidade da corrente livre.
Passo 1
Fala galerinha do coração!! Vamos fazer uma questãozinha de verdadeiro ou falso para fixar ainda mais nossos conhecimentos sobre a camada limite, ok? Partiu!!
Vamos avaliar cada uma das alternativas, começando com a primeira que diz que a camada limite é a região adjacente a uma superfície sólida na qual tensões viscosas estão presentes, em contraposição à corrente livre onde as tensões viscosas são desprezíveis…
Vamos lembrar lá do nosso exemplo, se temos um escoamento sobre um sólido existe uma fina camada onde as forças de atrito não podem ser ignoradas e lá é justamente a nossa querida camada limite… Então, essa opção é Verdadeira!
A segunda afirmação diz pra gente que as tensões viscosas presentes na camada limite são decorrentes do cisalhamento das camadas do fluido… Baseado no que acabamos de ver e lembrando que quanto mais distante do sólido a gente estiver menos sentiremos o efeito das tensões viscosas, concluímos que essa opção é Verdadeira!
A terceira opção diz que os gradientes de velocidade na camada limite originam tensões viscosas nesta região… Bom, de acordo com as duas opções anteriores, já sabemos que essa opção é Verdadeira também!
A quarta opção fala que na camada limite laminar existem gradientes de velocidade, os quais não estão presentes na camada turbulenta… Opa! Aí tem treta! Acabamos de dizer que quanto mais próximo ao sólido temos maiores efeitos de atrito, ou seja temos gradientes de velocidade presente, e essa opção está dizendo o contrário, logo essa opção é Falsa!
E a última opção tá afirmando que a espessura da camada limite pode ser definida como sendo a distância da superfície na qual a velocidade situa-se dentro de 1% da velocidade da corrente livre… Se a gente considera, nas definições, que a espessura da corrente livre é 99% da velocidade, logo a camada limite será de 1%, e portanto opção é Verdadeira!
Resposta
( V ) A camada limite é a região adjacente a uma superfície sólida na qual tensões viscosas estão presentes, em contraposição à corrente livre onde as tensões viscosas são desprezíveis.
( V ) As tensões viscosas presentes na camada limite são decorrentes do cisalhamento das camadas do fluido.
( V ) Gradientes de velocidade na camada limite originam tensões viscosas nesta região.
( F ) Na camada limite laminar existem gradientes de velocidade, os quais não estão presentes na camada turbulenta.
( V ) A espessura da camada limite pode ser definida como sendo a distância da superfície na qual a velocidade situa-se dentro de 1% da velocidade da corrente livre.
Sendo assim, a espessura da camada limite pode ser dada por:
Sendo a viscosidade, o comprimento do escoamento, a massa específica do fluido e o a velocidade do escoamento.
Olhando então para essa conclusão, vemos que a espessura da camada limite é diretamente proporcional ao comprimento do escoamento, que por sua vez está ligado a injeção de matéria, tranquilo?
Mas e o efeito disso no nosso fluxo de massa? Bom a gente viu que a transferência de massa por convecção é equivalente ao fluxo molar dividido pelas concentrações do escoamento:
Logo, se a gente aumenta a quantidade de matéria, aumentamos a concentração, então vamos diminuir nosso coeficiente convectivo… Opa! Então isso quer dizer que o aumento de matéria diminui o fuxo de massa convectiva.
Exercício Resolvido #6
Lista de exercícios sobre convecção mássica.
Use os resultados de Novais e Laurindo (1992) para Shp em leito fixo de esferas de naftaleno para verificar qual correlação é mais precisa.
Dado:

Passo 1
Fala aí! Bom vimos dois tipos de correlações que envolvem os nossos dados, né? Vamos fazer as contas para as duas e ver qual melhor se aproxima dos valores de Sherwood na tabela… Vamos nessa!
Pra começar temos que , então temos que usar as correlações que seja com essa condição, ok?
A primeira é a seguinte:
E a segunda:
Vamos partir para as continhas, com a primeira correlação:
Passo 2
Agora vamos fazer o mesmo para a segunda correlação:
Bom, vamos começar vendo que nenhuma dessas duas correlações se adequa bem ao modelo… Contudo, comparando os resultados vemos que a segunda correlação é a que mais se aproxima dos valores experimentais dados no enunciado.
Prontinho!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Elaboração própria.
Encontre o fluxo molar de um escoamento em uma tubulação de 28 cm de comprimento e 50 cm de diâmetro. Sabendo que o perfil de concentrações varia de 0,20 a 0,002 com a espessura do escoamento e que a difusividade mássica é de .
Dado: .
Passo 1
Fala aí! O enunciado quer da gente o fluxo molar, , certo? E ele nos deu o seguinte:
Comprimento da tubulação:
Difusividade mássica:
Concentração inicial:
Concentração na superfície livre:
Além do número de Sherwood, claro!
Bom, vamos lembrar lá da nossa teoria quando vimos de onde partiu nossas correlações para o número de Sherwood, ok? Dá só uma olhada aqui:
Então temos que:
Opa! Então o fluxo pode ser dado por:
Substituindo nossos dados, temos:
Ficamos então com um fluxo igual a:
Show de bolinhas!
Resposta
Exercício Resolvido #8
Elaboração própria.
Encontre o coeficiente de transferência de massa de um escoamento em uma tubulação de 28 cm de diâmetro e 10 km de comprimento. Sabendo que o perfil de concentrações varia de 0,69 a 0,080 com a espessura do escoamento.
Dado:
Passo 1
Fala aí! O enunciado quer o coeficiente de transferência de massa, né? Podemos encontrá-lo pela relação:
Opa! Precisamos antes de tudo encontrar o fluxo molar, , certo?
Nossos dados são:
Além do número de Sherwood, claro! rs
O nosso fluxo pode ser dado por:
Então ficaremos com:
Agora com o fluxo e com as concentrações, vamos entrar o coeficiente convectivo de massa:
Prontinho!