Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Convecção Natural

Ver Todos os Exercícios

Teoria

Fala aí! Hoje vamos trocar uma ideia sobre convecção natural. Tem muita diferença dessa pra tal da convecção forçada? E o que a gente faz quando a questão da prova envolver esses dois tipos?

Vem comigo descobrir tudo isso!

👇 Não deixe de conferir os tópicos anteriores a esse conteúdo 👇

Qual é a diferença entre convecção natural e convecção forçada?

Não tem muito segredo não, pra começar, ambos são mecanismos de transferência de calor.

A convecção forçada é aquela em que o movimento do fluido se deve a algum esforço ou mecanismo externo (como um ventilador, ou uma bomba).

Enquanto, na convecção natural, esse movimento se deve unicamente a propriedades internas do fluido (como diferenças de temperaturas, densidade e empuxo).

Beleza, com esses conceitos claros na cabeça, bora ver quais as novidades práticas nas nossas resoluções de exercícios!

Parâmetros Adimensionais para a Convecção Natural

Têm alguns parâmetros que são extremamente importante conhecermos pros nossos cálculos. Aqui no Responde Aí, já temos uma página tratando de cada um com mais detalhes, então só vou dar uma revisada bem básica, beleza?

Número de Nusselt

O número de Nusselt () é a forma adimensional do coeficiente de transferência de calor por convecção (). A expressão desse cara é a seguinte:

👉 é o comprimento característico.

👉 é a condutividade térmica do fluido.

Número de Reynolds

O número de Reynolds () é um parâmetro adimensional que relaciona as forças de inércia às forças viscosas em um fluido.

O número de Reynolds serve para determinar se um escoamento é laminar ou turbulento, o que é muito importante para o cálculo do número de Nusselt.

Uma das expressões para esse cara é a seguinte:

👉 é a massa específica do fluido.

👉 é a viscosidade dinâmica.

👉 é a velocidade no centro do escoamento.

👉 é o diâmetro do duto.

Número de Prandt

O número de Prandtl () é a razão entre as difusividades de momento e térmica.

Esse número é tabelado, então não precisa se preocupar tanto com o cálculo dele!

Número de Rayleigh

Esse cara aqui é novidade!

O número de Rayleigh () vai ser usado para determinar a correlação adequada para o número de Nusselt.

Já já te explico essa tal de correlação 😉.

As equações que vamos usar são essas aqui ó:

O é o número de Prandtl, de valor tabelado, e o outro termo, , é chamado número de Grashof. Esse último tem essa definição aqui:

👉 é a aceleração da gravidade.

👉 é a temperatura superficial do corpo imerso.

👉 é a temperatura do fluido.

👉 é o comprimento característico do corpo.

👉 é a viscosidade cinemática do fluido à temperatura de filme.

👉 é o coeficiente de expansão volumétrica, equivalente ao inverso da temperatura de filme.

Como resolver problemas de convecção natural

Para resolver problemas de convecção natural, vamos seguir o seguinte passo a passo:

  1. Pegar as propriedades do fluido à temperatura de filme nas tabelas.
  2. Calcular .
  3. Calcular o número de Grashof.
  4. Calcular o número de Rayleigh.
  5. Escolher a correlação adequada para o número de Nusselt a partir da geometria do corpo e do número de Rayleigh.
  6. Calcular o coeficiente convectivo.

Correlações para o Número de Nusselt

Beleza, eu falei tanto sobre escolher correlação adequada, mas o que raios isso quer dizer?

Correlações para Escoamentos externos

Vou deixar aqui uma tabela com uma série de correlações e quais os requisitos para utilizá-las. Para escoamentos externos, as seguintes são válidas:

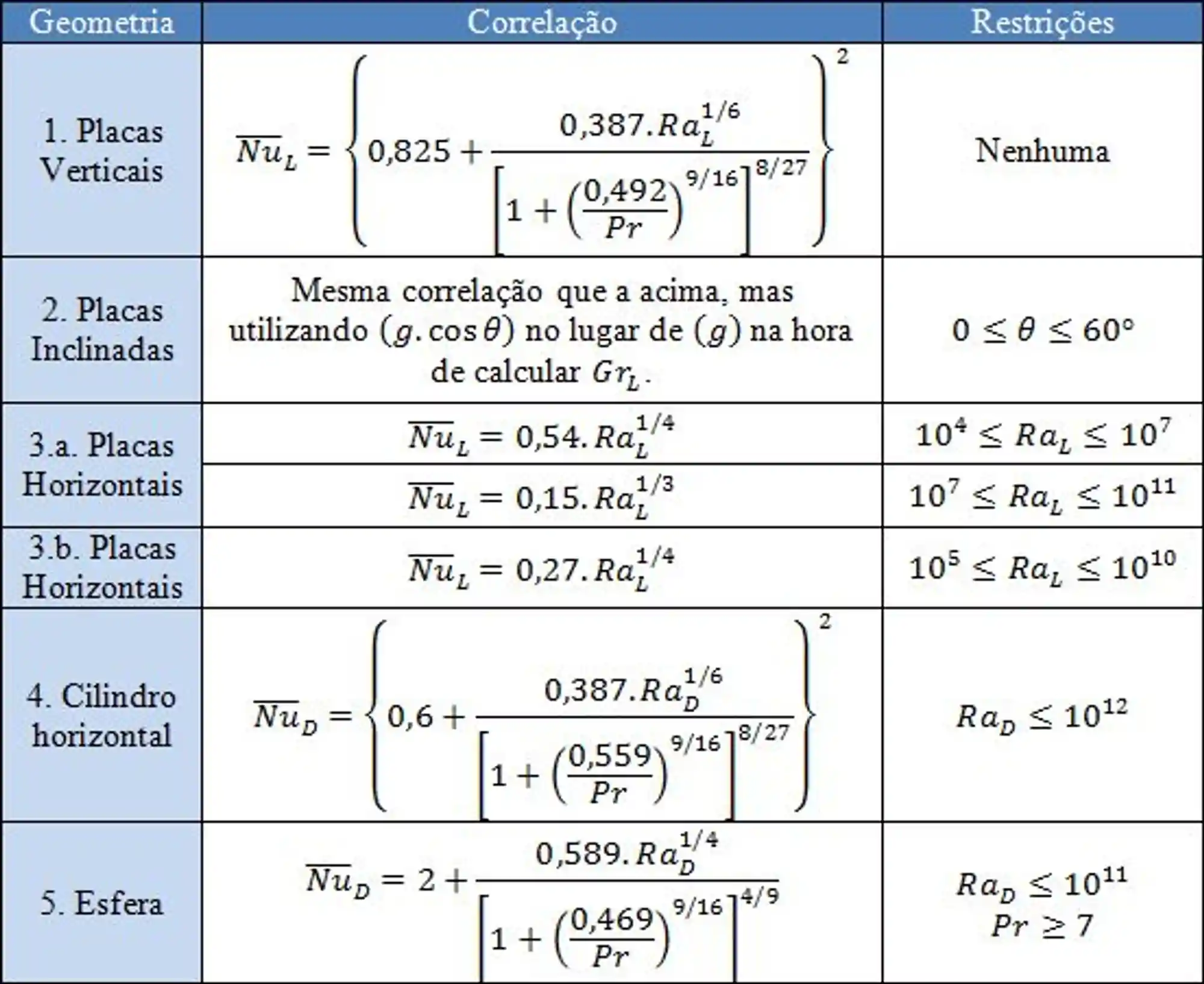
Tabela de correlações e restrições para o número de Nusselt.
Tabela de correlações e restrições para o número de Nusselt.

E cada uma dessas situações tão ilustradas aqui embaixo 👇

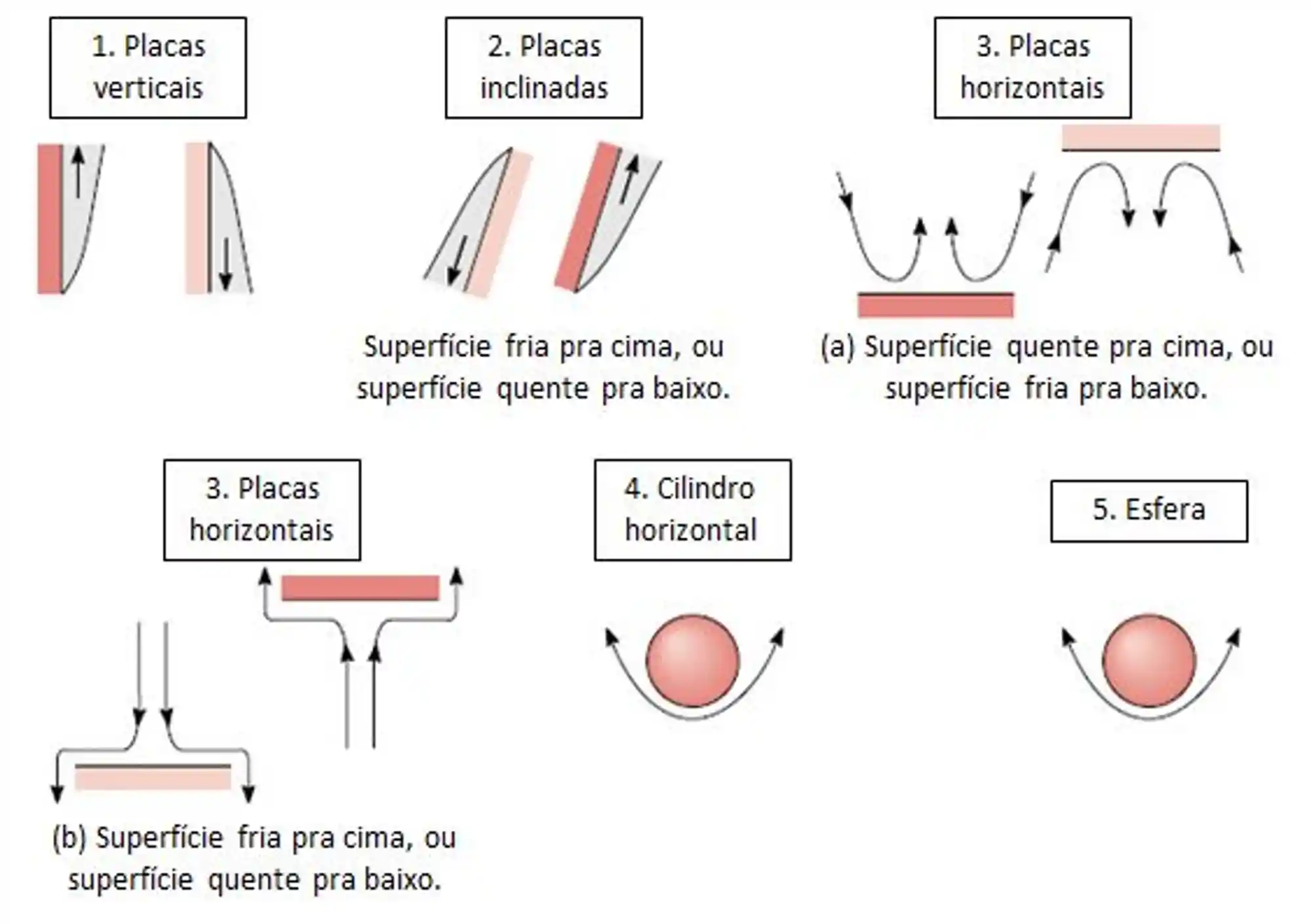
Ilustração de cada situação referente à tabela anterior.
Ilustração de cada situação referente à tabela anterior.

Correlações para Escoamentos em Canais

Aqui fica um pouquinho mais simples, pois só teremos duas situações: canais verticais e canais inclinados.

Em canais verticais, se as placas forem isotérmicas, o número de Rayleigh () e o número de Nusselt () serão dados por:

E essas constantes e são dadas por:

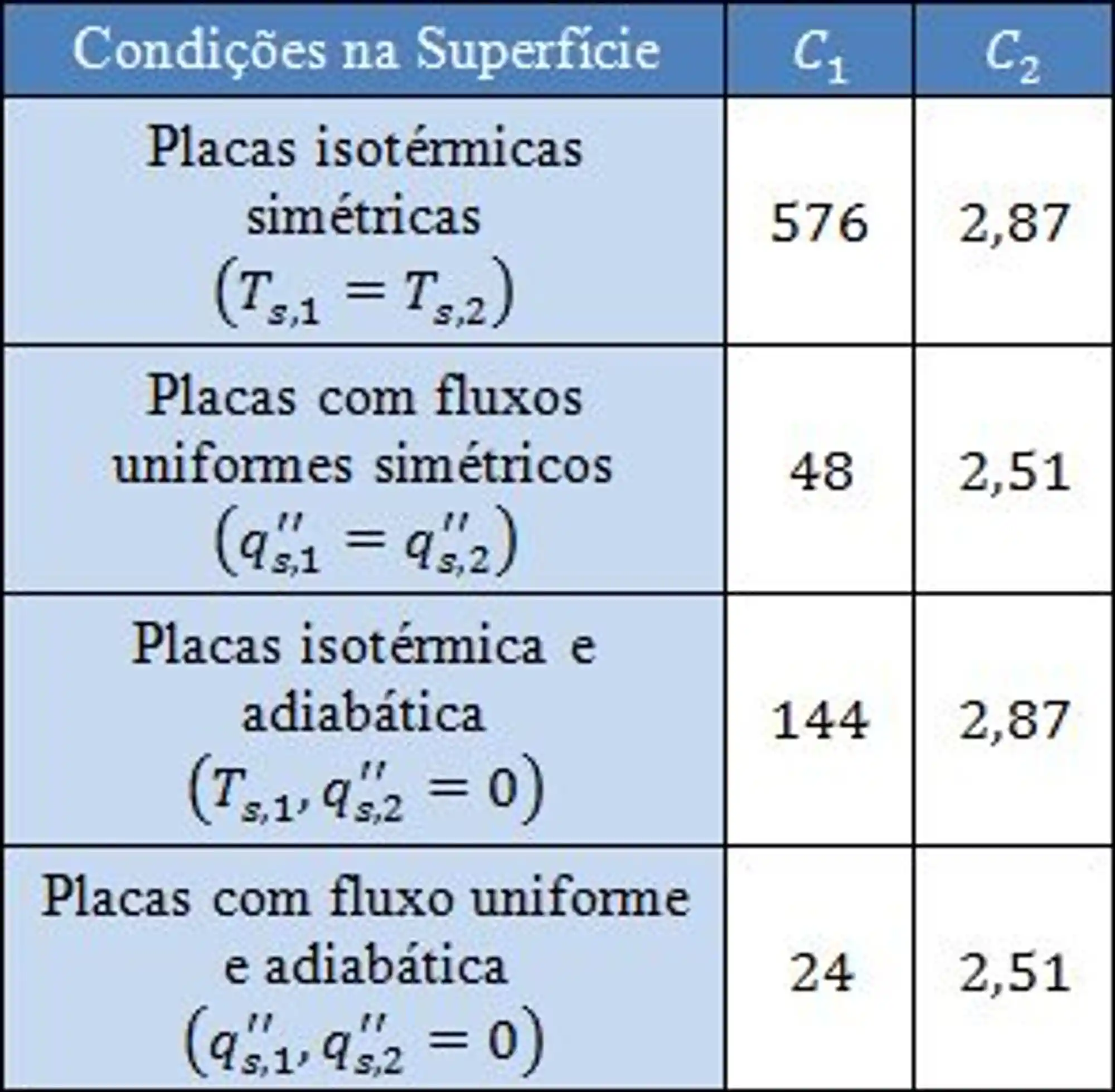
Tabela de constantes.
Tabela de constantes.

Já para os canais inclinados, temos somente essa correlação mais tranquila aqui:

Belezinha? É muita informação, né? Então bora praticar pra deixar tudo isso aí bem fixado!

Como resolver problemas de convecção natural

Correlações para o Número de Nusselt

Exercícios Resolvidos

Exercício Resolvido #1

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

(Adaptada) Considere uma janela simples (com uma única lâmina de vidro) vertical com largura e altura iguais W = L = 1   m . A superfície interior está exposta ao ar e às paredes do quarto, que estão a 18 ° C .

Sob condições ambientais frias, nas quais uma fina camada de gelo se forma na sua superfície interna, qual é a perda de calor através da janela? A emissividade do gelo pode ser considerada igual a ε = 0,9 .

Passo 1

Antes de qualquer coisa, vamos determinar as propriedades do ar para a temperatura de filme T f = T ∞ + T s 2 = 9 ° C = 282 K . De acordo com a tabela A.4 do Incropera, temos que:

k = 0,0249   W / ( m . K )

υ = 14,3 × 10 - 6   m 2 / s

α = 20,1 × 10 - 6   m 2 / s

P r = 0,712

β = 1 T f = 3,55 × 10 - 3   K - 1

Agora podemos seguir em frente.

Passo 2

A taxa de transferência total de calor q na janela será igual à soma das taxas de transferência de calor por convecção livre q c o n r e por radiação q r a d . Se liga:

q = q c o n v + q r a d

q = h - . A . T ∞ - T s + ε . σ . A . T s u r 4 - T s 4

Onde:

A = W × L = 1   m 2

T ∞ = 18 ° C = 291   K

T s = 0 ° C = 273   K

T s u r = 18 ° C = 291   K

ε = 0,9

σ = 5,61 × 10 - 8   W / m 2

Opa! O único termo que não temos dessa equação é o coeficiente convectivo h - , então vamos atrás dele.

Passo 3

O coeficiente convectivo está associado ao número de Nusselt por:

h - = N u - L . k L

Como estamos trabalhando com uma placa vertical, a correlação mais adequada para o número de Nusselt será:

N u - L = 0,825 + 0,387 . R a L 1 / 6 1 + 0,492 P r 9 / 16 8 / 27 2

Onde o número de Rayleigh é dado por:

R a L = g β T ∞ - T s L 3 α υ

Substituindo os valores:

R a L = 9,8 × 3,55 × 10 - 3 × 291 - 273 × 1 3 14,3 × 10 - 6 × 20,1 × 10 - 6 → R a L = 2,18 × 10 9

Substituindo na expressão do número de Nusselt:

N u - L = 0,825 + 0,387 . 2,18 × 10 9 1 / 6 1 + 0,492 0,712 9 / 16 8 / 27 2 → N u - L = 156,5

Finalmente o coeficiente convectivo será:

h - = 156,5 × 0,0249 1 → h - = 3,9   W / ( m 2 . K )

Passo 4

Agora estamos prontos pra calcular a taxa de transferência de calor total:

q = h - . A . T ∞ - T s + ε . σ . A . T s u r 4 - T s 4

Substituindo os valores:

q = 3,9 × 1 × 291 - 273 + 0,9 × 5,67 × 10 - 8 × 1 × 291 4 - 273 4

Resposta

q = 152,7   W

Exercício Resolvido #2

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

Um aquecedor elétrico com a forma de um disco horizontal com 400   m m de diâmetro é usado para aquecer o fundo de um tanque de óleo de motor a uma temperatura de 5 ° C .

Calcule a potência necessária para manter a temperatura do aquecedor a 70 ° C .

Passo 1

Antes de qualquer coisa, vamos determinar as propriedades do óleo para a temperatura de filme:

T f = T ∞ + T s 2 = 37,5 ° C = 310,5   K

Para essa temperatura, de acordo com a tabela A.5 do Incropera, temos que:

k = 0,145   W / ( m . K )

υ = 288 . 10 - 6   m 2 / s

α = 0,847 . 10 - 7   m 2 / s

β = 0,70 . 10 - 3   K - 1

Obs.: Para o óleo, o valor de β também é dado na tabela.

Agora podemos seguir em frente.

Passo 2

Para calcular a taxa de transferência de calor, precisamos calcular o coeficiente convectivo médio através do número de Nusselt.

h - = N u - L . k L

Como o disco está no fundo do tanque, estamos trabalhando com placas horizontais do tipo a (lá da tabela da teoria). Vamos calcular o R a L pra determinar qual N u - L usar.

O número de Rayleigh é dado por:

R a L = g β T ∞ - T s L 3 α υ

Nesse caso, com a placa é circular, a dimensão L deve ser calculada com a razão entre a área e o perímetro da placa, se liga:

L = π D 2 / 4 π D = D 4 = 0,4 4 → L = 0,1 m

Substituindo os valores:

R a L = 9,8 . 0,7 . 10 - 3 . 70 - 5 . 0,1 3 288 . 10 - 6 . 0,847 . 10 - 7 → R a L = 1,828 . 10 7

E, com:

10 7 ≤ R a L ≤ 10 11

Vamos ter:

N u - L = 0,15 . R a L 1 / 3

N u - L = 0,15 . 1,828 . 10 7 1 / 3 → N u - L = 39,5

Finalmente o coeficiente convectivo será:

h - = 39,5 . 0,145 0,1 → h - = 57,3   W / ( m 2 . K )

Passo 3

A taxa de transferência de calor será dada por:

q = h - . A . T ∞ - T s

Substituindo os valores:

q = 57,3 . π . 0,4 2 4 . 70 - 5

Resposta

q = 468   W

Exercício Resolvido #3

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

Uma placa com dimensões de 1   m por 1   m e inclinada com um ângulo de 45 ° , tem a sua superfície inferior exposta a um fluxo t��rmico radiante líquido de 300   W / m 2 .

Se a superfície superior da placa for bem isolada, estime a temperatura que a placa atingirá quando o ar ambiente estiver quiescente a uma temperatura de 0 ° C .

Passo 1

Como não temos a temperatura superficial da placa, vamos precisar chutar um valor inicial pra poder determinar as propriedades do ar. Se, ao final das contas, virmos que o nosso chute foi muito ruim, o certo será refazer as contas, agora considerando o valor que encontramos como chute.

Sendo assim, vamos chutar que a placa esteja a uma temperatura superficial de T s = 84 ° C , dessa forma, a temperatura de filme será:

T f = 84 + 0 2 = 42 ° C = 315   K

De acordo com a tabela A.4 do Incropera, teremos:

υ = 17,4 × 10 - 6   m 2 / s  

k = 0,0274   W / ( m . K )

α = 24,7 × 10 - 6   m 2 / s

P r = 0,705

β = 1 T f = 1 315 = 3,17 × 10 - 3   K - 1

Passo 2

Para calcular a temperatura superficial, podemos usar a seguinte expressão:

q ' ' = h - L . T s - T ∞ → T s = T ∞ + q ' ' h - L

Agora precisamos calcular o coeficiente convectivo.

Passo 3

O coeficiente convectivo será dado por:

h - L = k . N u - L L

Onde, como estamos trabalhando com uma placa inclinada, o número de Nusselt será dado por:

N u - L = 0,825 + 0,387 . R a L 1 / 6 1 + 0,492 P r 9 / 16 8 / 27 2

Sendo o número de Rayleigh:

R a L = g . cos ⁡ θ . β T s - T ∞ L 3 α υ

Substituindo os valores:

R a L = 9,8 × cos ⁡ 45 ° × 3,17 × 10 - 3 × 84 - 0 × 1 3 24,7 × 10 - 6 × 17,4 × 10 - 6

R a L = 4,3 × 10 9

Assim, o número de Nusselt será:

N u - L = 0,825 + 0,387 . 4,3 × 10 9 1 / 6 1 + 0,492 0,705 9 / 16 8 / 27 2

N u - L = 193,2

Assim, o coeficiente convectivo será:

h - L = 0,0274 × 193,2 1 → h - L = 5,29   W / ( m 2 . K )

Passo 4

Finalmente, a temperatura da placa será:

T s = T ∞ + q ' ' h - L = 0 + 300 5,29

Resposta

T s = 57 ° C

Exercício Resolvido #4

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

Um bastão horizontal com 5   m m de diâmetro está imerso em água mantida a 18 ° C . Se a temperatura superficial do bastão é de 56 ° C , estime a taxa de transferência de calor por convecção natural por unidade de comprimento do bastão.

Passo 1

Nosso primeiro passo é determinar as propriedades da água para a temperatura de filme T f = T ∞ + T s 2 = 37 ° C = 310   K . De acordo com a tabela A.6 do Incropera, temos que:

k = 0,628   W / ( m . K )

υ = 7 × 10 - 7   m 2 / s

α = 1,514 × 10 - 7   m 2 / s

β = 361,9 × 10 - 6   K - 1

P r = 4,62

Obs.: Para a água, o valor de β também é dado na tabela.

Agora podemos seguir em frente.

Passo 2

Para calcular a taxa de transferência de calor, precisamos calcular o coeficiente convectivo médio através do número de Nusselt.

h - D = N u - D . k L

Nesse caso, como estamos trabalhando com um cilindro, o número de Nusselt é dado por:

N u - D = 0,6 + 0,387 . R a D 1 / 6 1 + 0,559 P r 9 / 16 8 / 27 2

Onde o número de Rayleigh é dado por:

R a D = g β T ∞ - T s D 3 α υ

Substituindo os valores:

R a D = 9,8 × 361,9 × 10 - 6 × 56 - 18 × 0,005 3 7 × 10 - 7 × 1,514 × 10 - 7 → R a L = 1,587 × 10 5

Substituindo na expressão do número de Nusselt:

N u - D = 0,6 + 0,387 × 1,587 × 10 5 1 / 6 1 + 0,559 4,62 9 / 16 8 / 27 2 → N u - D = 10,4

Finalmente o coeficiente convectivo será:

h - D = 10,4 × 0,628 0,005 → h - = 1306   W / ( m 2 . K )

Passo 3

A taxa de transferência de calor por unidade de comprimento q ' será dada por:

q ' = h - . π D . T ∞ - T s

Substituindo os valores:

q ' = 1306 × π × 0,005 × 56 - 18

Resposta

q ' = 780   W / m

Exercício Resolvido #5

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

Sob condições de operação em regime estacionário, a temperatura superficial de uma pequena lâmpada incandescente de 20   W é de 125 ° C , quando as temperaturas do ar ambiente e das paredes são iguais a 25 ° C .

Aproximando a lâmpada por uma esfera de 40   m m de diâmetro e com emissividade na superfície de 0,8 , qual é a taxa de transferência de calor saindo da superfície da lâmpada?

Passo 1

Nosso primeiro passo é determinar as propriedades do ar para a temperatura de filme T f = ( T ∞ + T s ) / 2 = 75 ° C = 348   K . De acordo com a tabela A.4 do Incropera, temos que:

k = 0,0298   W / ( m . K )

υ = 20,72 × 10 - 6   m 2 / s

α = 29,6 × 10 - 6   m 2 / s

P r = 0,7

β = 1 T f = 1 348 = 2,87 × 10 - 3   K - 1

Agora podemos seguir em frente.

Passo 2

A taxa total de transferência de calor q será dada pela soma das taxas de transferência de calor por convecção natural q c o n v e por radiação q r a d .

q = q c o n v + q r a d

Substituindo as expressões das taxas de transferência de calor:

q = h - D . A . T s - T ∞ + ε . σ . A . T s 4 - T ∞ 4

Onde A = 4 π r 2 = π D 2 .

Dessa expressão, nós temos basicamente todo mundo, com exceção do coeficiente convectivo médio. Então vamos atrás desse cara.

Passo 3

Vamos calcular o coeficiente convectivo médio através do número de Nusselt.

h - D = N u - D . k L

Nesse caso, como estamos trabalhando com uma esfera, o número de Nusselt é dado por:

N u - D = 2 + 0,589 . R a D 1 / 4 1 + 0,469 P r 9 / 16 4 / 9

Onde o número de Rayleigh é dado por:

R a D = g β T ∞ - T s D 3 α υ

Substituindo os valores:

R a D = 9,8 × 2,87 × 10 - 3 × 125 - 25 × 0,04 3 20,72 × 10 - 6 × 29,6 × 10 - 6 → R a L = 2,93 × 10 5

Substituindo na expressão do número de Nusselt:

N u - D = 2 + 0,589 × 2,93 × 10 5 1 / 4 1 + 0,469 0,7 9 / 16 4 / 9 → N u - D = 12,5 6

Finalmente o coeficiente convectivo será:

h - D = 12,5 6 × 0,0298 0,04 → h - = 9,36   W / ( m 2 . K )

Passo 4

Voltando à taxa de transferência de calor, temos o seguinte:

q = h - D . A . T s - T ∞ + ε . σ . A . T s 4 - T ∞ 4

Substituindo os valores:

q = 9,36 × π × 0,04 2 × 125 - 25 + 08 × 5,67 × 10 - 8 × π × 0,04 2 × 125 + 273 4 - 25 + 273 4

q = 8,62   W

Resposta

q = 8,62   W

Exercício Resolvido #6

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

(Adaptado) Uma esfera de cobre com 25   m m de diâmetro, com um revestimento de baixa emissividade, é removida de um forno a uma temperatura uniforme de 85 ° C e deixada resfriar em um fluido quiescente mantido a 25 ° C .

Calcule os coeficientes convectivos associados às condições iniciais para a imersão no ar e na água.

Passo 1

Logo de cara vamos determinar as propriedades do ar e da água à temperatura de filme, dada por:

T f = T s + T ∞ 2 = 85 + 25 2 → T f = 55 ° C = 328   K

De acordo com a tabela A.4, as propriedades do ar a esta temperatura são:

υ = 1,871 × 10 - 5   m 2 / s

k = 0,0284   W / ( m . K )

α = 2,66 × 10 - 5   m 2 / s

P r = 0,703

β = 1 T f = 3,05 × 10 - 3   K - 1

De acordo com a tabela A.6, as propriedades da água a esta temperatura são:

υ = 5,121 × 10 - 7   m 2 / s

k = 0 , 648   W / ( m . K )

α = 1,57 × 10 - 7   m 2 / s

P r = 3,26

β = 4,909 × 10 - 4   K - 1

Passo 2

Os coeficientes convectivos são dados por:

h - D = k . N u - D D

Como estamos trabalhando com uma esfera, o número de Nusselt será dado por:

N u - D = 2 + 0,589 . R a D 1 / 4 1 + 0,469 P r 9 / 16 4 / 9

Onde o número de Rayleigh é dado por:

R a D = g β T ∞ - T s D 3 α υ

Agora é só calcular o coeficiente convectivo para cada caso.

Passo 3

Para o ar, teremos:

R a D = g β T ∞ - T s D 3 α υ = 9,8 × 3,05 × 10 - 3 × 85 - 25 × 0,025 3 2,66 × 10 - 5 × 1,871 × 10 - 5

R a D = 56282

Assim, o número de Nusselt será:

N u - D = 2 + 0,589 × 56282 1 / 4 1 + 0,469 0,703 9 / 16 4 / 9

N u - D = 8,99

Finalmente, o coeficiente convectivo será:

h - D = k . N u - D D = 0,0284 × 8,99 0,025

Passo 4

Para a água:

R a D = g β T ∞ - T s D 3 α υ = 9,8 × 4,909 × 10 - 4 × 85 - 25 × 0,025 3 1,57 × 10 - 7 × 5,121 × 10 - 7

R a D = 5,6 × 10 7

Assim, o número de Nusselt será:

N u - D = 2 + 0,589 × 5,6 × 10 7 1 / 4 1 + 0,469 3,26 9 / 16 4 / 9

N u - D = 46,8

Finalmente, o coeficiente convectivo será:

h - D = k . N u - D D = 0,648 × 46,8 0,025

Resposta

Ar: h - D = 10,2   W / ( m 2 . K )

Água: h - D = 1213   W / ( m 2 . K )

Exercício Resolvido #7

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

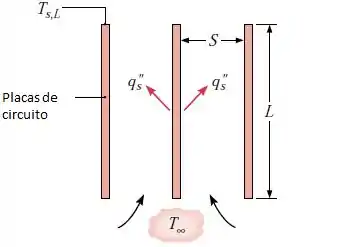
Um série de placas de circuitos verticais encontra-se imersa em ar ambiente quiescente a T ∞ = 17 ° C . Embora os componentes sejam salientes em relação aos substratos, é razoável, em uma primeira aproximação, considerar placas planas com fluxo térmico na superfície uniforme q s ' ' .

Considere placas com comprimento e largura L = W = 0,4   m e espaçamento S = 25   m m . Se a temperatura máxima admissível na placa é de 77 ° C , qual é a potência máxima que pode ser dissipada por placa?

Passo 1

Esse é um problema de escoamento em canal vertical em que temos fluxo constante em ambas as placas, pra resolvê-lo vamos ter que utilizar a seguinte correlação para o número de Nusselt:

N u s , L = C 1 R a s * S L + C 2 R a s * S L 2 / 5 - 1 / 2

Onde R a s * é dado por:

R a S * = g . β . q s ' ' . S 4 k . α . υ

Assim, vamos precisar pegar algumas propriedades do ar à temperatura de filme T f = T s + T ∞ / 2 = 47 ° C = 320 K .

υ = 17,9 × 10 - 6   m 2 / s

k = 0,0278   W / ( m . K )

α = 25,5 × 10 - 6   m 2 / s  

β = 1 320 = 3,125 × 10 - 3   K - 1

Agora podemos seguir em frente!

Passo 2

Substituindo os valores, o número de Rayleigh será dado por:

R a S * = g . β . q s ' ' . S 4 k . α . υ = 9,8 × 3,15 × 10 - 3 × 0,025 4 × q s ' ' 0,0278 × 25,5 × 10 - 6 × 17,9 × 10 - 6

R a S * = 942,75 . q s ' '

Substituindo na expressão do número de Nusselt, teremos:

N u s , L = C 1 R a s * S L + C 2 R a s * S L 2 / 5 - 1 / 2

Como estávamos trabalhando com uma situação em que as placas tem fluxos térmicos simétricos: C 1 = 48 e C 2 = 2,51 . Logo:

N u s , L = 48 942,75 × q s ' ' × 0,025 0,4 + 2,51 942,75 × q s ' ' × 0,025 0,4 2 / 5 - 1 / 2

N u s , L = 0,815 q s ' ' + 0,492 q s ' ' 2 / 5 - 1 / 2

Show! Agora vamos tentar encontrar outra expressão para o número de Nusselt.

Passo 3

O número de Nusselt está associado ao coeficiente convectivo através da seguinte equação:

h = N u s , L . k S

Esse mesmo coeficiente convectivo está associado ao fluxo de calor da seguinte forma:

q s ' ' = h . T s - T ∞

Opa! Se substituirmos a expressão do coeficiente convectivo na expressão acima, teremos o seguinte:

q s ' ' = N u s , L . k S . T s - T ∞

Se reorganizarmos esse cara pra isolar o número de Nusselt, teremos:

N u s , L = q s ' ' T s - T ∞ S k

Substituindo os valores:

N u s , L = 0,025 × q s ' ' 77 - 17 × 0,0278

N u s , L = 0,015 . q s ' '

Opa! Agora basta igualar as duas expressões pra encontrarmos o valor do fluxo térmico.

Passo 4

0,015 . q s ' ' = 0,815 q s ' ' + 0,492 q s ' ' 2 / 5 - 1 / 2

Agora não tem muito jeito, o fluxo térmico é calculado por tentativa e erro. Nesse caso, vamos encontrar que:

q s ' ' = 287   W / m 2

Passo 5

Pra fechar, como queremos calcular a taxa de transferência de calor, basta multiplicar o fluxo pela área das placas:

q = 2 q s ' ' . A = 2 × 287 × 0,4 2

Resposta

q = 91,8   W

Exercício Resolvido #8

ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.

Um tanque cilíndrico de propano de 1,5   m de diâmetro e 4   m de comprimento é inicialmente cheio com propano líquido, cuja densidade é 581   k g / m 3 . O reservatório é exposto ao ar ambiente a 25 ° C em condições meteorológicas calmas.

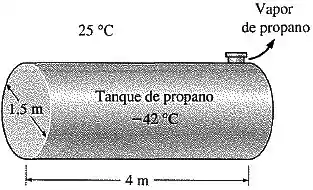
A superfície externa do tanque é polida de modo que a transferência de calor por radiação é desprezível. Agora, uma rachadura se desenvolve na parte superior do tanque e a pressão no interior cai para 1   a t m enquanto a temperatura cai para - 42 ° C , que é a temperatura de ebulição do propano a 1   a t m .

O calor de vaporização do propano a 1   a t m é 425   k J / k g . O propano é lentamente vaporizado como resultado da transferência de calor do ar ambiente para o reservatório e seu vapor escapa do tanque a - 42 ° C através da rachadura.

Considerando que o tanque de propano está mais ou menos na mesma temperatura que o propano em seu interior, em qualquer momento, determine quanto tempo vai demorar para o tanque esvaziar se ele não estiver isolado.

Passo 1

Antes de qualquer coisa, vamos determinar as propriedade do ar à temperatura de filme, dada por:

T f = T s + T ∞ 2 = - 42 + 25 2 → T f = - 8,5 ° C

De acordo com a tabela A.4 do Incropera, a essa temperatura:

k = 0,02299   W / ( m . ° C )

υ = 1,265 × 10 - 5   m 2 / s

P r = 0,7383

Além disso, o coeficiente de expansão volumétrica térmica é dado por:

β = 1 T f = 1 - 8,5 + 273 → β = 0,003781   K - 1

Passo 2

Inicialmente, temos uma massa m de propano, dada por:

m = ρ . V = ρ . π . D 2 4 . L = 581 × π × 1,5 2 × 4 4 → m = 4107   k g

A massa de propano passa a evaporar a uma taxa m ˙ , dada por:

q = m ˙ . h v → m ˙ = q h v

Onde q = h - D . A . T s - T ∞ .

m ˙ = h - D . A . T ∞ - T s h v

Onde m ˙ e m estão associados por:

m ˙ = m Δ t → Δ t = m m ˙

Dessa brincadeira toda, o único cara que não temos é o coeficiente convectivo. Vamos atrás dele então.

Passo 3

O coeficiente convectivo é dado por:

h - D = k . N u - D D

Para cilindros, o número de Nusselt é dado por:

N u - D = 0,6 + 0,387 . R a D 1 / 6 1 + 0,559 P r 9 / 16 8 / 27 2

Onde o número de Rayleigh é dado por:

R a D = g β T ∞ - T s D 3 υ 2 . P r

Substituindo os valores:

R a D = 9,8 × 0,003781 × 25 - - 42 × 1,5 3 1,265 × 10 - 5 2 × 0,7383 → R a L = 3,869 × 10 10

Substituindo na expressão do número de Nusselt:

N u - D = 0,6 + 0,387 × 3,869 × 10 10 1 / 6 1 + 0,559 0,7383 9 / 16 8 / 27 2 → N u - D = 374,1

Finalmente o coeficiente convectivo será:

h - D = 0,02299 × 374,1 1 , 5 → h - D = 5,733   W / ( m 2 . K )

Passo 4

Assim, a vazão mássica de propano será:

m ˙ = h - D . A . T ∞ - T s h v

Onde:

A = π D L + 2 . π D 2 4 = π × 1,5 × 4 + 2 π × 1,5 2 4 → A = 22,38   m 2

Logo:

m ˙ = 5,733 × 22,38 × 25 - - 42 425 → m ˙ = 0,02023   k g / s

Passo 5

Finalmente, o tempo necessário pra esvaziar o tanque será:

Δ t = m m ˙ = 4107 0,02023

Δ t = 203015   s

Resposta

Δ t = 56,4   h o r a s

Exercício Resolvido #9

Questão 3, PUC, P3-2003

(Adaptado) Considere uma placa plana horizontal aquecida por meio de uma resistência elétrica. A superfície inferior da placa é isolada e a superior troca calor por convecção com o ambiente, que está a 25 ° C . A placa tem comprimento igual a 3   m e largura igual a 1,5   m .

Considere as propriedades do ar iguais a k = 0,025   W / m K , υ = 20,92 × 10 - 6   m 2 / s , α = 30 × 10 - 6   m 2 / s . Calcule a taxa de transferência de calor trocado por convecção e radiação, onde a potência fornecida pela resistência elétrica mantém a placa à temperatura de 100 ° C .

Passo 1

Esse é um problema de convecção natura, onde o coeficiente de expansão volumétrica térmica é dado por:

β = 1 T f = 1 T s + T ∞ 2 = 2 100 + 273 + 25 + 273

β = 2,98 × 10 - 3   K - 1

Passo 2

O número de Rayleigh é dado por:

R a L = g β T ∞ - T s L 3 α υ

Substituindo os valores:

R a L = 9,8 1 × 2,98 × 10 - 3 × 373 - 2 98 × 3 3 30 × 10 - 6 × 20,92 × 10 - 6

R a L = 9,43 × 10 10

Passo 3

Como estamos trabalhando com um caso de placa horizontal, para o valor de número de Rayleigh que encontramos, a correlação mais adequada para o número de Reynolds é dada por:

N u L - = 0,15 . R a L 1 / 3 = 0,15 × 9,43 × 10 10 1 / 3

N u L - = 682,75

O coeficiente convectivo será:

h - = N u L - . k L = 682,75 × 0,025 3

h - = 5,69   W / m 2 K

Passo 4

A taxa de transferência de calor será:

q = h - . A . T s - T ∞ = 5,69 × 3 × 1,5 × 100 - 25

Resposta

q = 1920,23   W

Exercício Resolvido #10

Questão 1, UFF, P2-2016.2

(Adaptado) Um conjunto de placas quadradas de circuitos verticais com 150   m m de altura deve ser resfriado com ar em meio a uma sala grande de tal maneira que a temperatura nas placas não seja superior a 60 ° C , quando a temperatura ambiente é de 30 ° C .

Admitindo condições de superfícies isotérmicas, determine a dissipação de potência elétrica admissível (fluxo de calor) por placa quando não há nenhum escoamento forçado de ar.

Passo 1

Vamos começar determinando as propriedades do ar para a temperatura de filme T f = T ∞ + T s 2 = 45 ° C = 318 K . De acordo com a tabela A.4 do Incropera, temos que:

k = 0,02 76   W / ( m . K )

υ = 17,7 × 10 - 6   m 2 / s

α = 25,2 × 10 - 6   m 2 / s

P r = 0,7 05

β = 1 T f = 3 , 14 × 10 - 3   K - 1

Agora podemos seguir em frente.

Passo 2

O fluxo de calor é dado por:

q = h - . A . T s - T ∞

Onde A = 0,15 2 = 0,0225   m 2 . O único termo dessa equação que não temos e o coeficiente convectivo. Então vamos atrás dele.

Passo 3

O coeficiente convectivo é dado por:

h - = N u - L . k L

Como estamos trabalhando com uma placa vertical, a correlação mais adequada para o número de Nusselt será:

N u - L = 0,825 + 0,387 . R a L 1 / 6 1 + 0,492 P r 9 / 16 8 / 27 2

Onde o número de Rayleigh é dado por:

R a L = g β T s - T ∞ L 3 α υ

Substituindo os valores:

R a L = 9,8 × 3 , 14 × 10 - 3 × 60 - 30 × 0,15 3 25,2 × 10 - 6 × 17,7 × 10 - 6 → R a L = 4,65 × 10 7

Substituindo na expressão do número de Nusselt:

N u - L = 0,825 + 0,387 × 4,65 × 10 7 1 / 6 1 + 0,492 0,705 9 / 16 8 / 27 2 → N u - L = 48,65

Finalmente o coeficiente convectivo será:

h - = 48,65 × 0,0276 0,15 → h - = 8,95   W / ( m 2 . K )

Passo 4

Agora estamos prontos pra calcular fluxo de calor:

q = h - . A . T ∞ - T s

Substituindo os valores:

q = 8,95   × 0,0225 × 60 - 30

Resposta

q = 6,04   W

Exercício Resolvido #11

Questão 2, UFF, P2-2017.1

Uma esfera de 1   m m de diâmetro de aço inoxidável 316 está a 600 K . A esfera foi posta para esfriar em meio ao ar em um ambiente inicialmente quiescente.

A temperatura do ar é 275 K , a pressão é a pressão ambiente. As propriedades do ar podem ser aproximadas pelas propriedades do ar, como gás ideal, a 275 K .

Determine quanto tempo levará para que o interior (centro) da esfera esfrie até a temperatura de 298 K .

Passo 1

Antes de avaliarmos qual é o melhor método para calcular o tempo necessário para que o centro da esfera se resfrie, precisamos calcular o número de Biot, dado por:

B i = h D - . L c k = h D - . D 6 k

Onde, de acordo com a tabela A.6, para a temperatura de 600   K :

k = 18,3   W / ( m . K )

c p = 550   J / ( k g . K )

ρ = 8238   k g / m 3

Pra calcular o número de Biot, vamos precisar calcular o coeficiente convectivo dessa bagaça.

Passo 2

Esse se trata de um problema de convecção livre, onde as propriedades do ar, de acordo com a tabela A.4 do Incropera, considerando a temperatura de 275   K será dada por:

k = 0,0242   W / ( m . K )

υ = 13,67 × 10 - 6   m 2 / s

α = 19,2 × 10 - 6   m 2 / s

P r = 0,7 13

Para o valor de β , devemos considerar a temperatura de filme, dada por:

T f = T ∞ + T s 2

Como a temperatura superficial também irá variar, vamos considera-la como a média entre as temperaturas inicial de final da esfera.

T s = 600 + 298 2 = 449   K

β = 1 T f = 1 449 = 2,23 × 10 - 3   K - 1

Agora podemos seguir em frente.

Passo 3

Vamos calcular o coeficiente convectivo médio através do número de Nusselt.

h - D = N u - D . k D

Nesse caso, como estamos trabalhando com uma esfera, o n��mero de Nusselt é dado por:

N u - D = 2 + 0,589 . R a D 1 / 4 1 + 0,469 P r 9 / 16 4 / 9

Onde o número de Rayleigh é dado por:

R a D = g β T s - T ∞ D 3 α υ

Substituindo os valores:

R a D = 9,8 × 3,63 × 10 - 3 × 449 - 275 × 0,001 3 19,2 × 10 - 6 × 13,67 × 10 - 6 → R a D = 23,6

Substituindo na expressão do número de Nusselt:

N u - D = 2 + 0,589 × 23,6 1 / 6 1 + 0,469 0,7 13 9 / 16 4 / 9 → N u - D = 2,77

Finalmente o coeficiente convectivo será:

h - D = 2,77 × 0,0242 0,0 01 → h - = 67,03     W / ( m 2 . K )

Passo 4

Assim, o número de Biot será:

B i = h D - . D 6 k = 67,03 × 0,001 6 × 18,3

B i = 6,1 × 10 - 4 < 0,1

Opa! Com esse valor, podemos usar o Método dos Parâmetros Concentrados. De acordo com esse método, o tempo necessário para resfriar a esfera será:

t = ρ . V . c p h D - . A . ln ⁡ T i - T ∞ T t - T ∞

Onde a razão V / A vale:

V A = 4 π r 3 3 4 π r 2 = r 3 = D 6

Logo:

t = ρ . D . c p 6 . h D - . ln ⁡ T i - T ∞ T t - T ∞

t = 8238 × 0,001 × 550 6 × 67,03 × ln ⁡ 600 - 275 298 - 275

Resposta

t = 29,8   s

Exercícios de Livros Relacionados

67 - Um programa de computador está sendo desenvolvido para analisar um sensor cilíndrico, com 12,5 mm de diâmetro, utilizado para determinar a temperatura do ar ambiente. O sensor experimenta convecç
As superfícies de dois longos tubos horizontais concêntricos, com paredes delgadas e raios de 100m m e 125m m , são mantidas a 300K e 400K , respectivamente. Sendo a região anular pressurizada com nit
Um objeto quente suspenso por uma corda deve ser resfriado por convecção natural em fluidos cujos volumes mudam de maneira diferente com a temperatura à pressão constante. Em qual fluido a taxa de res
Considere uma janela de painel duplo composta por duas folhas de vidro separadas por um espaço de ar de 1 cm de largura. Alguém sugere a inserção de uma fina folha de vinil no meio dos dois vidros par
Um reservatório retangular de 28 cm de altura, 18 cm de comprimento e 18 cm de largura suspenso em uma sala a 24 °C é inicialmente preenchido com água fria a 2 °C. A temperatura da superfície do reser