Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 105
As superfícies de dois longos tubos horizontais concêntricos, com paredes delgadas e raios de e , são mantidas a e , respectivamente. Sendo a região anular pressurizada com nitrogênio a , estime a taxa de transferência de calor convectiva, por unidade de comprimento dos tubos.
Passo 1
Vamos começar esquematizando nossa situação:
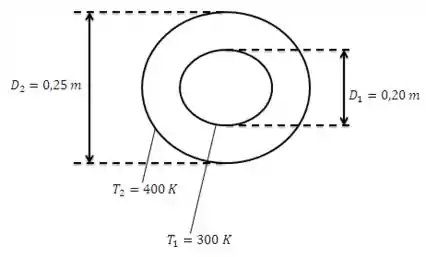
Temos dois tubos concêntricos, com nitrogênio a contido no espaço entre eles. Sabemos as dimensões dos tubos ( e ) e as temperaturas da superfície dos tubos e ) e, a partir destes dados devemos obter a taxa de transferência de calor por convecção natural. Vamos lá?
Como primeiro passo vamos calcular a temperatura média do nitrogênio e obter suas propriedades. A temperatura média será:
Para esta temperatura as propriedades do nitrogênio são (Tabela A-4, apêndice A):
Passo 2
Nosso próximo passo será obter o comprimento característico para este problema. Em um espaço cilíndrico confinado ele é dado por:
A partir do comprimento característico e das propriedades do nitrogênio podemos determinar o número de Rayleigh:
Passo 3
Agora, iremos aplicar a correlação de condutividade térmica efetiva para um espaço cilíndrico fechado:
Por fim, vamos usar a equação de taxa de transferência de calor por convecção natural:
Resposta
A taxa de transferência de calor por unidade de comprimento de tubulação é .