Escoamento em uma Matriz de Tubos
Produzido por Giovanna RonzéTeoria
Introdução
A ideia aqui é basicamente a seguinte: enquanto um fluido (em preto) se move sobre os tubos, outro fluido (em azul) escoa no interior dos tubos.
Por enquanto, estamos interessados somente na transferência de calor por convecção do fluido em preto, que escoa sobre os tubos. Em um outro momento, vamos nos preocupar com o fluido que escoa no interior dos tubos. ;)
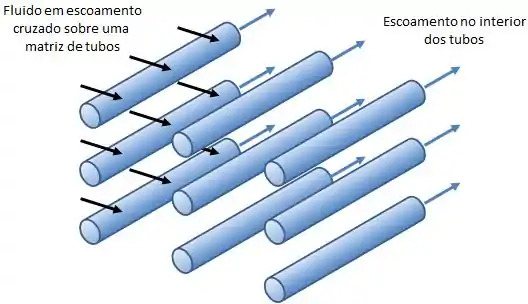
As fileiras dos tubos podem estar alinhadas, ou alternadas, se liga:
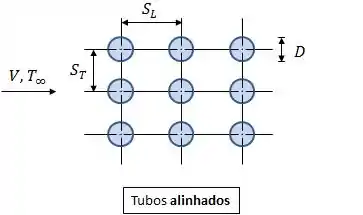
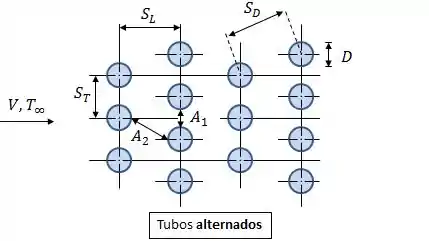
Relaxa! Vou te explicar o que é cada coisa aqui, beleza?
Nessa configuração, é o diâmetro dos tubos, é o passo transversal e é o passo longitudinal. Essas três grandezas são as que caracterizam a configuração dos tubos.
A medida é basicamente a diagonal, calculada a partir dos passos e . Pra finalizar, e representam os planos onde o fluido vai passar, e são muito importantes na hora de calculamos o número de Reynolds.
“Peraí! Vamos ter que calcular o número de Reynolds de outra forma?!”

Opa! A pergunta é boa! Vamos dar uma atenção a isso, então.
O que muda na hora de calcular o número de Reynolds?!
Bom, a fórmula em si do número de Reynolds continua bem parecida com o que estamos acostumados:
![]()
O que muda aqui é que, agora, não vamos mais considerar a velocidade de escoamento livre. No lugar dela, vamos passar a considerar a velocidade máxima de escoamento .
E é justamente aqui que entra a questão dos planos e por onde o fluido vai passar, porque a velocidade vai ser máxima justamente em um deles, no caso do arranjo com tubos alternados.
Para o arranjo alinhado, a velocidade será máxima em , e é dada por:
![]()
Para o arranjo alternado, a velocidade será máxima em se:
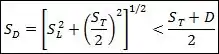
Nesse caso, a velocidade máxima será dada por:
![]()
Caso contrário, se a relação abaixo não for verdadeira:
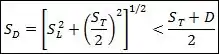
Você vai usar a fórmula pra velocidade máxima em . Ou seja:
![]()
Então, a malandragem é essa! Se o arranjo for alternado, use a nossa regrinha para saber se a velocidade é máxima em ou . Depois, calcule a velocidade máxima e, por último, calcule o número de Reynolds.
Agora já podemos seguir em frente. :)
Correlação de Zukauskas
Essa é a única correlação que usaremos para resolver problemas com escoamento em uma matriz de tubos. Ela é dada por:
![]()
Onde as constantes e são dadas pela tabela abaixo:
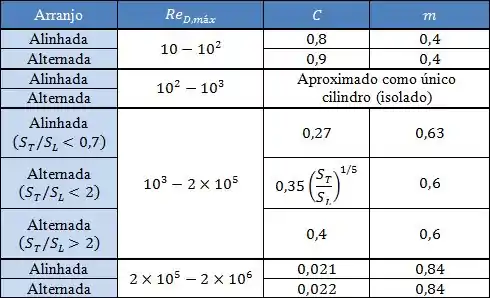
Essa correlação é válida para:
Onde corresponde ao número de colunas de tubos.
Aqui, nós estamos calculando todos esses caras para o escoamento livre. Ou seja, para o escoamento do lado de fora dos tubos. Mas esse que aparece na fórmula, é o número de Prandtl calculado para a temperatura da superfície dos tubos. Essa é a única diferença.
“Beleza! Mas e se tivermos um problema onde o número de colunas é menor que 20?!”
Cara, muito boa mesmo a pergunta!
Bom, nesse caso, a gente multiplica o número de Nusselt por uma constante, que vamos chamar de , se liga:
![]()
Onde para .
Os valores de para são dados na tabela abaixo:

Nesse caso, como calculamos a taxa de transferência de calor?!
Para esse caso, nós costumamos calcular a taxa de transferência de calor por unidade de comprimento dos tubos , dada por:
Onde:
: Número total de tubos;
: Coeficiente convectivo médio, calculado através no números de Nusselt médio ;
: Diâmetro dos tubos;
: Média logarítmica das diferenças de temperatura.
Apareceu alguém aí que ainda não tinha chegado na festa! A média logarítmica das diferenças de temperatura é dada por:
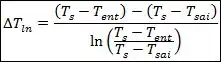
Essa expressão é bem comum quando se trabalha com trocadores de calor.
“Tá! E se eu não tiver a temperatura de saída?!”
Bem, nesse caso, nós podemos estima-la através da seguinte equação:
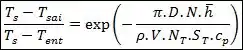
Nessa equação é o número de tubos no plano transversal.
Vamos fixar isso melhor nos exercícios?!
O que muda na hora de calcular o número de Reynolds?!
Correlação de Zukauskas
Nesse caso, como calculamos a taxa de transferência de calor?!
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Um preaquecedor utiliza vapor d’água saturado a , alimentado pelo lado interno dos tubos de uma matriz, para preaquecer ar que entra no sistema a e .
Ar escoa em escoamento cruzado no lado externo dos tubos a . Cada tubo possui de comprimento e de diâmetro externo. A matriz contém 196 tubos e um arranjo alinhado quadrado, no qual .
Qual é a taxa de transferência de calor total para o ar?
Passo 1
Antes de qualquer coisa, vamos determinar as propriedades do ar para resolver o problema.
De acordo com a tabela A.4 do Incropera para o ar a , temos que:
À temperatura da superfície , temos que .
Passo 2
A taxa de transferência de calor é dada por:
Logo:
Dessa equação, nos temos praticamente tudo, menos o coeficiente convectivo médio e a temperatura de saída , que vamos precisar pra calcular a média logarítmica das temperaturas.
A temperatura de saída é dada por:
Arrumando essa equação, vamos encontrar o seguinte:
Obs.: Agora vamos ter que ir atrás do coeficiente convectivo médio.
Passo 3
O número de Nusselt, dado por:
Como a matriz possui uma configuração alinhada:
Para esse valor de número de Reynolds, temos que:
Além disso, como , de acordo com a tabela na Teoria . Logo, o número de Nusselt será:
Passo 4
O coeficiente convectivo será dado por:
Voltando à expressão da temperatura de saída.
Substituindo os valores:
Passo 5
Voltando à expressão da taxa de transferência de calor por unidade de comprimento, temos:
Onde a média logarítmica de temperaturas é dada por:
Substituindo os valores:
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6 ed.
(Adaptada) Seja uma matriz alinhada de tubos de , , e , com vapor d’água em condensação usado para aquecer ar atmosférico entrando na matriz a e .
Qual é o valor mínimo de necessário para atingir uma temperatura de saída ?
Passo 1
Antes de qualquer coisa, vamos determinar as propriedades do ar.
Como temos a temperatura de entrada e saída, vamos determinar as propriedades do ar à temperatura média entre as duas. Logo:
A essa temperatura, de acordo com a tabela A.4 do Incropera:
Para a temperatura de superfície , temos .
Passo 2
A temperatura de saída pode ser obtida através dessa expressão:
Onde . Assim, reorganizando a expressão acima, isolando , teremos:
Daqui, temos basicamente tudo, exceto o coeficiente convectivo. Então vamos calculá-lo!
Passo 3
O número de Nusselt, dado por:
Como a matriz possui uma configuração alinhada:
Para esse valor de número de Reynolds, temos que:
Além disso, supondo . O número de Nusselt será:
Passo 4
O coeficiente convectivo será, finalmente:
Voltando à expressão de :
Substituindo os valores:
Como é um número inteiro, o valor mínimo de será:
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Uma matriz tubular utiliza um arranjo alinhado com tubos de de diâmetro com . Existem 10 fileiras de tubos contendo 50 tubos cada uma.
Considere uma aplicação na qual água fria escoa através dos tubos, mantendo uma temperatura na superfície externa dos tubos de , enquanto gases de exaustão, a e a uma velocidade de , escoam em escoamento cruzado na matriz.
As propriedades dos gases de exaustão podem ser aproximadas pelas do ar atmosférico a .
Qual é a taxa de transferência de calor total, por unidade de comprimento dos tubos, no feixe?
Passo 1
Antes de qualquer coisa, vamos tratar de buscar as propriedades do ar pra resolver o problema.
De acordo com a tabela A.4 do Incropera, para a temperatura de , temos que:
E para a temperatura temos o seguinte:
Agora vamos partir pro problema.
Passo 2
Então, a taxa de transferência de calor total, por unidade de comprimento dos tubos é dada por:
Dessa equação, nos temos praticamente tudo, menos o coeficiente convectivo médio e a temperatura de saída , que vamos precisar pra calcular a média logarítmica das temperaturas.
A temperatura de saída é dada por:
Se reorganizarmos essa equação, vamos encontrar o seguinte:
Obs.: Agora não tem pra onde fugir, vamos atrás do coeficiente convectivo médio.
Passo 3
O número de Nusselt, dado por:
Como a matriz possui uma configuração alinhada:
Para esse valor de número de Reynolds, temos que:
Além disso, como , de acordo com a tabela na Teoria . Logo, o número de Nusselt será:
Passo 4
O coeficiente convectivo será, finalmente:
Voltando à expressão da temperatura de saída.
Substituindo os valores:
Passo 5
Voltando à expressão da taxa de transferência de calor por unidade de comprimento, temos:
Onde a média logarítmica de temperaturas é dada por:
Substituindo os valores:
![]()
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptada) Uma matriz de tubos possui um arranjo alinhado com tubos de de diâmetro e de comprimento, com . Existem 10 colunas de tubos na direção do escoamento e 7 tubos por coluna .
Ar, com condições a montante da matriz iguais a e , escoa em escoamento cruzado sobre os tubos, cujas paredes são mantidas a pela condensação de vapor no seu interior.
Determine a temperatura do ar ao deixar a matriz tubular.
Passo 1
Antes de qualquer coisa, vamos pegar na tabela A.4 do Incropera as propriedades do ar a .
Para o ar a , temos .
Agora podemos seguir em frente.
Passo 2
Como queremos saber a temperatura se saída do ar, podemos usar essa equação aqui:
Se reorganizarmos essa equação, vamos encontrar o seguinte:
Obs.: Temos quase tudo aqui, com exceção do coeficiente convectivo médio.
Então vamos atrás dele.
Passo 3
O número de Nusselt, dado por:
Como a matriz possui uma configuração alinhada:
Para esse valor de número de Reynolds, temos que:
Além disso, como , de acordo com a tabela na Teoria . Logo, o número de Nusselt será:
Passo 4
O coeficiente convectivo será, finalmente:
Voltando à expressão da temperatura de saída.
Substituindo os valores:
![]()
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptada) Um condensador resfriado a ar opera com ar em escoamento cruzado sobre uma matriz quadrada composta por 400 tubos alinhados . O diâmetro externo dos tubos é de e os passos longitudinal e transversal na matriz tubular são e , respectivamente.
Vapor d’água saturado a uma pressão de entra nos tubos e pode-se considerar que uma temperatura uniforme de seja mantida na superfície externa dos tubos em função da condensação no seu interior.
Se a temperatura e a velocidade da corrente de ar a montante da matriz tubular são e , qual é a temperatura do ar que deixa a matriz? Como uma primeira aproximação, avalie as propriedades do ar a .
Se os tubos possuírem de comprimento, qual é a taxa de transferência de calor total na matriz?
Passo 1
Vamos começar levantando as propriedades que vamos usar para resolver para resolver a questão.
Para o ar, de acordo com a tabela A.4 do Incropera, usando como referência :
Para o ar à temperatura , temos .
Passo 2
Se a temperatura e a velocidade da corrente de ar a montante da matriz tubular são e , qual é a temperatura do ar que deixa a matriz? Como uma primeira aproximação, avalie as propriedades do ar a .
Como não temos a temperatura de saída, a mesma pode ser estimada através da seguinte equação:
Se reorganizarmos essa equação, vamos encontrar o seguinte:
Dessa equação, nós temos quase tudo, falta justamente o coeficiente convectivo médio.
Então vamos cuidar disso.
Passo 3
Pra calcular o coeficiente convectivo, precisamos do número de Nusselt, dado por:
Como a matriz possui uma configuração alinhada:
Para esse valor de número de Reynolds, precisamos calcular a razão entre os passos pra saber os valore de e mais adequados:
Para esses valores, temos que:
Além disso, como , . Logo, o número de Nusselt será:
Passo 4
O coeficiente convectivo será, finalmente:
Voltando à expressão da temperatura de saída.
Substituindo os valores:
![]()
Passo 5
Se os tubos possuírem de comprimento, qual é a taxa de transferência de calor total na matriz? Qual é a taxa de condensação do vapor em ?
A taxa de transferência de calor por unidade de comprimento é dada por:
Assim, a taxa de transferência de calor total será dada por:
Onde a média logarítmica de temperaturas é dada por:
Substituindo os valores:
![]()
Resposta
Exercício Resolvido #6
Questão 3, PUCRIO, P2-2005
Considere o escoamento de ar sobre um feixe de tubos alinhados, de acordo com a figura.
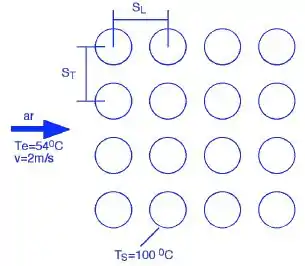
Dentro dos tubos escoa vapor d’água, a temperatura de . Os tubos têm diâmetro igual a e comprimento de . A distância entre os centros dos tubos vale . O ar entra a e . Sabe-se que o número de tubos na direção do escoamento é igual ao na direção transversal . Determine o menor número de tubos necessários para que a temperatura de saída do ar seja maior do que . Calcule a taxa de transferência de calor trocado entre o ar e os tubos. Despreze a resistência a condução nos tubos (i.e., considere que a temperatura na parede é igual a temperatura do vapor).
Passo 1
A primeira coisa que temos que fazer é determinar as propriedades do ar.
Como temos a temperatura de entrada e saída, vamos determinar as propriedades do fluido à temperatura média entre as duas. Assim:
Aproximando essa temperatura para , de acordo coma tabela A.4 do Incropera:
Já a , de acordo com a tabela A.4 do Incropera:
Obs.: Os dados foram obtidos através de interpolações, feitas diretamente na calculadora.
Passo 2
A temperatura de saída pode ser obtida através dessa expressão:
Onde . Assim, reorganizando a expressão acima, isolando , teremos:
Daqui, temos basicamente tudo, exceto o coeficiente convectivo. Então vamos calcula-lo!
Passo 3
O número de Nusselt, dado por:
Como a matriz possui uma configuração alinhada:
Para esse valor de número de Reynolds, temos que:
Além disso, supondo . O número de Nusselt será:
Passo 4
O coeficiente convectivo será, finalmente:
Voltando à expressão de :
Substituindo os valores:
Como é um número inteiro, o valor mínimo de será:
Finalmente, o número total de tubos será:
![]()
Passo 5
A taxa de transferência de calor será dada por:
Onde vale:
Substituindo os valores:
![]()
Resposta
Exercício Resolvido #7
Questão 2, UFF, P2-2015.2
(Adaptado) Uma superfície quadrada de de lado está posta sobre uma circuito gerador de energia térmica que mantém a superfície referida a . Essa superfície possui sobre ela um conjunto de pinos circulares.
São 25 pinos dispostos em 5 fileiras de 5 pinos. Os pinos possuem de diâmetro, de comprimento e estão distribuídos uniformemente a partir de um pino central localizado no centro da placa e espaçados igualmente de (distância entre as fileiras e os pinos da mesma fileira).
Existe um escoamento externo com ar a que escoa perpendicularmente a esse conjunto de pinos a uma velocidade de .
Determine a perda de calor do sistema e diga se o sistema foi bem dimensionado ou não, justificando sua resposta.
As propriedades termofísicas do ar são consideradas constantes e dadas pelo valor delas a .
Passo 1
Antes de qualquer coisa, vamos determinar as propriedades do ar. De acordo com a tabela A.4, para o ar a , temos:
Para a temperatura de superfície , temos .
Passo 2
A taxa de transferência de calor é dada por:
Dessa equação, nos temos praticamente tudo, menos o coeficiente convectivo médio e a temperatura de saída , que vamos precisar pra calcular a média logarítmica das temperaturas.
A temperatura de saída é dada por:
Arrumando essa equação, vamos encontrar o seguinte:
Não tem pra onde correr, vamos ter que ir atrás do coeficiente convectivo médio.
Passo 3
O número de Nusselt, dado por:
Como a matriz possui uma configuração alinhada:
Nesse caso, o problema nos deu que a distância entre os tubos é de e que o diâmetro dos tubos é de .
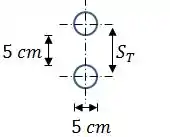
Dessa forma, os passos serão ambos iguais a . Logo:
Para esse valor de número de Reynolds, temos que:
Além disso, como , de acordo com a tabela na Teoria . Logo, o número de Nusselt será:
Passo 4
O coeficiente convectivo será dado por:
Voltando à expressão da temperatura de saída.
Substituindo os valores:
Passo 5
Voltando à expressão da taxa de transferência de calor por unidade de comprimento, temos:
Onde a média logarítmica de temperaturas é dada por:
Substituindo os valores:
![]()